题目内容
下列命题中,命题正确的是( )A.终边相同的角一定相等
B.第一象限的角是锐角
C.若α-β=2kπ(k∈z),则角α的三角函数值等于角β的同名三角函数值
D.半径为R,n°的圆心角所对的弧长为R•n°
【答案】分析:用排除法解决问题,由终边相同的角相差周角的整数倍,可排除A;用 来说明B的错误;用弧长公式来排除D,即可得到正确答案.
来说明B的错误;用弧长公式来排除D,即可得到正确答案.
解答:解:由终边相同的角的性质,终边相同的角相差周角的整数倍,不一定相等,故A错误;
 为第一象限的角,但不是锐角,故B错误;
为第一象限的角,但不是锐角,故B错误;
半径为R,n°的圆心角所对的弧长为R• ,故D错误;
,故D错误;
故选C
点评:本题考查的知识点是利用终边相同的角的定义和性质,结合象限角与轴线角的定义及弧长公式,判断命题的真假,要判断一个命题为真命题,我们可以使用排除法进行解答.
 来说明B的错误;用弧长公式来排除D,即可得到正确答案.
来说明B的错误;用弧长公式来排除D,即可得到正确答案.解答:解:由终边相同的角的性质,终边相同的角相差周角的整数倍,不一定相等,故A错误;
 为第一象限的角,但不是锐角,故B错误;
为第一象限的角,但不是锐角,故B错误;半径为R,n°的圆心角所对的弧长为R•
 ,故D错误;
,故D错误;故选C
点评:本题考查的知识点是利用终边相同的角的定义和性质,结合象限角与轴线角的定义及弧长公式,判断命题的真假,要判断一个命题为真命题,我们可以使用排除法进行解答.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
下列命题中,命题正确的是( )
| A、终边相同的角一定相等 | B、第一象限的角是锐角 | C、若α-β=2kπ(k∈z),则角α的三角函数值等于角β的同名三角函数值 | D、半径为R,n°的圆心角所对的弧长为R•n° |

 “
“ ,使得
,使得 ”,则
”,则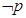 是真命题.
是真命题. ,则
,则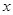 ,
,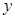 互为相反数”的逆命题为假命题.
互为相反数”的逆命题为假命题. ”,则
”,则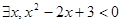 ”.
”.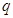 ”的逆否命题是“若
”的逆否命题是“若 ,则
,则 ”.
”.