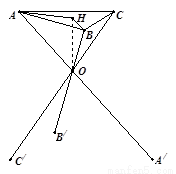题目内容
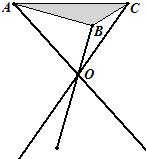 某厂根据市场需求开发折叠式小凳(如图所示)、凳面为三角形的尼龙布,凳脚为三根细钢管、考虑到钢管的受力和人的舒适度等因素,设计小凳应满足:①凳子高度为30cm,②三根细钢管相交处的节点O与凳面三角形ABC重心的连线垂直于凳面和地面.
某厂根据市场需求开发折叠式小凳(如图所示)、凳面为三角形的尼龙布,凳脚为三根细钢管、考虑到钢管的受力和人的舒适度等因素,设计小凳应满足:①凳子高度为30cm,②三根细钢管相交处的节点O与凳面三角形ABC重心的连线垂直于凳面和地面.(1)若凳面是边长为20cm的正三角形,三只凳脚与地面所成的角均为45°,确定节点O分细钢管上下两段的比值(精确到0.01);
(2)若凳面是顶角为120°的等腰三角形,腰长为24cm,节点O分细钢管上下两段之比为2:3、确定三根细钢管的长度(精确到0.1cm).
分析:(1)设△ABC的重心为H,连接OH,根据∠OBH就是OB与平面ABC所成的角,建立BH与OH的等量关系,解之即可;
(2)设∠B=120°,△ABC的重心为H,求出OH,分别在Rt△AHO,Rt△CHO,Rt△BHO中求出OA、OB、OC,再根据比例关系求出所求即可.
(2)设∠B=120°,△ABC的重心为H,求出OH,分别在Rt△AHO,Rt△CHO,Rt△BHO中求出OA、OB、OC,再根据比例关系求出所求即可.
解答: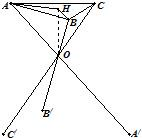 解:(1)设△ABC的重心为H,连接OH
解:(1)设△ABC的重心为H,连接OH
由题意可得,BH=
设细钢管上下两段之比为λ
已知凳子高度为30、则OH=
∵节点O与凳面三角形ABC重心的连线与地面垂直,且凳面与地面平行
∴∠OBH就是OB与平面ABC所成的角,亦即∠OBH=45°
∵BH=OH,∴
=
解得λ=
≈0.63
即节点O分细钢管上下两段的比值约为0.63
(2)设∠B=120°,∴AB=BC=24,AC=24
设△ABC的重心为H,则BH=8,AH=8
,
由节点O分细钢管上下两段之比为2:3,可知OH=12
设过点A、B、C的细钢管分别为AA'、BB'、CC',
则AA′=CC′=
OA=
=10
≈60.8,
BB′=
OB=
=10
≈36.1,
∴对应于A、B、C三点的三根细钢管长度分别为60.8cm,36.1cm和60.8cm
 解:(1)设△ABC的重心为H,连接OH
解:(1)设△ABC的重心为H,连接OH由题意可得,BH=
20
| ||
| 3 |
设细钢管上下两段之比为λ
已知凳子高度为30、则OH=
| 30λ |
| 1+λ |
∵节点O与凳面三角形ABC重心的连线与地面垂直,且凳面与地面平行
∴∠OBH就是OB与平面ABC所成的角,亦即∠OBH=45°
∵BH=OH,∴
| 30λ |
| 1+λ |
20
| ||
| 3 |
解得λ=
2
| ||
9-2
|
即节点O分细钢管上下两段的比值约为0.63
(2)设∠B=120°,∴AB=BC=24,AC=24
| 3 |
设△ABC的重心为H,则BH=8,AH=8
| 7 |
由节点O分细钢管上下两段之比为2:3,可知OH=12
设过点A、B、C的细钢管分别为AA'、BB'、CC',
则AA′=CC′=
| 5 |
| 2 |
| 5 |
| 2 |
| OH2+AH2 |
| 37 |
BB′=
| 5 |
| 2 |
| 5 |
| 2 |
| OH2+BH2 |
| 13 |
∴对应于A、B、C三点的三根细钢管长度分别为60.8cm,36.1cm和60.8cm
点评:本题主要考查了直线与平面所成的角,以及三角形重心的应用,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,② 三根细钢管相交处的节点
,② 三根细钢管相交处的节点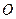 与凳面三角形
与凳面三角形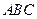 重心的连线垂直于凳面和地面. (1)若凳面是边长为
重心的连线垂直于凳面和地面. (1)若凳面是边长为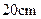 的正三角形,三只凳脚与地面所成的角均为
的正三角形,三只凳脚与地面所成的角均为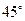 ,确定节点
,确定节点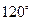 的等腰三角形,腰长为
的等腰三角形,腰长为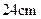 ,节点
,节点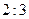 . 确定三根细钢管的长度.
. 确定三根细钢管的长度.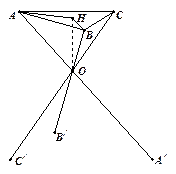
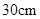 ,② 三根细钢管相交处的节点
,② 三根细钢管相交处的节点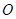 与凳面三角形
与凳面三角形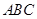 重心的连线垂直于凳面和地面. (1)若凳面是边长为
重心的连线垂直于凳面和地面. (1)若凳面是边长为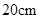 的正三角形,三只凳脚与地面所成的角均为
的正三角形,三只凳脚与地面所成的角均为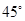 ,确定节点
,确定节点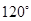 的等腰三角形,腰长为
的等腰三角形,腰长为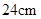 ,节点
,节点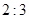 . 确定三根细钢管的长度.
. 确定三根细钢管的长度.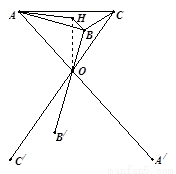
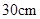 ,② 三根细钢管相交处的节点
,② 三根细钢管相交处的节点 与凳面三角形
与凳面三角形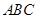 重心的连线垂直于凳面和地面. (1)若凳面是边长为
重心的连线垂直于凳面和地面. (1)若凳面是边长为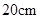 的正三角形,三只凳脚与地面所成的角均为
的正三角形,三只凳脚与地面所成的角均为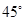 ,确定节点
,确定节点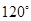 的等腰三角形,腰长为
的等腰三角形,腰长为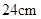 ,节点
,节点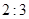 . 确定三根细钢管的长度.
. 确定三根细钢管的长度.