题目内容
(本题满分16分,其中第(1)小题4分,第(2)小题8分,第(3)小题4分)
设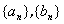 是两个数列,
是两个数列, 为直角坐标平面上的点.对
为直角坐标平面上的点.对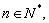 若三点
若三点 共线,
共线,
(1)求数列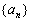 的通项公式;
的通项公式;
(2)若数列{ }满足:
}满足: ,其中
,其中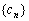 是第三项为8,公比为4的等比数列.求证:点列
是第三项为8,公比为4的等比数列.求证:点列 (1,
(1,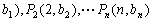 在同一条直线上;
在同一条直线上;
(3)记数列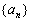 、{
、{ }的前
}的前 项和分别为
项和分别为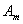 和
和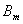 ,对任意自然数
,对任意自然数 ,是否总存在与
,是否总存在与 相关的自然数
相关的自然数 ,使得
,使得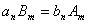 ?若存在,求出
?若存在,求出 与
与 的关系,若不存在,请说明理由.
的关系,若不存在,请说明理由.
【答案】
解:(1)因三点 共线,
共线, …………2分
…………2分
得 故数列
故数列 的通项公式为
的通项公式为  …………4分
…………4分
(2)由题意 ,
,
由题意得  …………6分
…………6分


当 时,
时, …………8分
…………8分


 .当n=1时,
.当n=1时, ,也适合上式,
,也适合上式,

 …………10分
…………10分
因为两点 的斜率
的斜率
 为常数
为常数
所以点列 (1,
(1, 在同一条直线上. …………12分
在同一条直线上. …………12分
(3)由 得
得 ;
;
 得
得 …………14分
…………14分
若 ,则
,则



 ∴
∴
∴对任意自然数 ,当
,当 时,总有
时,总有 成立。…………16分
成立。…………16分

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
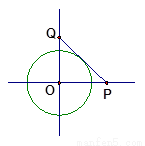
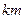 的圆形村落,A、B两人同时从村落中心O出发,B向北直行,A先向东直行,出村后不久,在点P处改变方向,沿着与村落周界相切的直线前进,后来恰与B在点Q处相遇.设A、B两人速度一定,其速度比为3:1,问Q距O多远?
的圆形村落,A、B两人同时从村落中心O出发,B向北直行,A先向东直行,出村后不久,在点P处改变方向,沿着与村落周界相切的直线前进,后来恰与B在点Q处相遇.设A、B两人速度一定,其速度比为3:1,问Q距O多远?
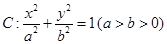 的一个焦点为
的一个焦点为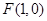 ,点
,点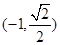 在椭圆
在椭圆 上,点
上,点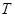 满足
满足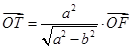 (其中
(其中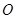 为坐标原点), 过点
为坐标原点), 过点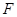 作一斜率为
作一斜率为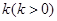 的直线交椭圆于
的直线交椭圆于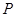 、
、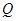 两点(其中
两点(其中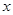 轴上方,
轴上方,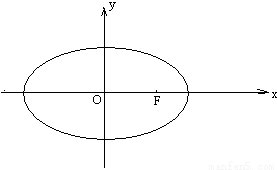
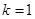 ,求
,求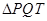 的面积;
的面积;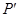 为点
为点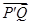 与
与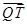 的位置关系,并说明理由.
的位置关系,并说明理由. ,试将此人按上述路线从A到C所需时间T表示为
,试将此人按上述路线从A到C所需时间T表示为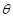 的函数;并求自变量
的函数;并求自变量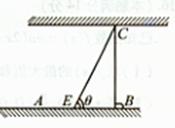
 ,其前
,其前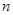 项和为
项和为 ,对任意
,对任意 都有:
都有:
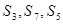 构成等差数列,求实数
构成等差数列,求实数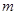 的值;
的值;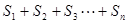 ,
,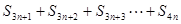 ,
, 不能构成等差数列.
不能构成等差数列.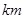 的圆形村落,A、B两人同时从村落中心O出发,B向北直行,A先向东直行,出村后不久,在点P处改变方向,沿着与村落周界相切的直线前进,后来恰与B在点Q处相遇.设A、B两人速度一定,其速度比为3:1,问Q距O多远?
的圆形村落,A、B两人同时从村落中心O出发,B向北直行,A先向东直行,出村后不久,在点P处改变方向,沿着与村落周界相切的直线前进,后来恰与B在点Q处相遇.设A、B两人速度一定,其速度比为3:1,问Q距O多远?