题目内容
已知 ,
,
(1)求 ;
;
(2)当k为何实数时, 与
与 平行,平行时它们是同向还是反向?
平行,平行时它们是同向还是反向?
解:(1)∵已知 ,
,
∴ =(8,6)
=(8,6)
∴ =
= ;
;
(2)因为 ,
, ,当
,当 与
与 平行,
平行,
则(k-4)×(8)-(4k-1)×6=0,解得: ,
,
此时 ,
,

= =
= =
=
- (10,4)=-
(10,4)=- (
(  +2
+2  ),
),
所以, 与
与 反向.
反向.
分析:(1)先根据条件求出向量 的坐标,再利用向量的模的计算公式求出其模即可,
的坐标,再利用向量的模的计算公式求出其模即可,
(2)当 与
与 平行时,有(k-3)×(-4)-(2k+2)×10=0,解得
平行时,有(k-3)×(-4)-(2k+2)×10=0,解得 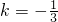 ,此时可得,
,此时可得,
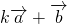 =-
=- (
(  -3
-3  ),故
),故  反向.
反向.
点评:本题考查两个向量共线的条件和性质,两个向量坐标形式的运算,求出k值,是解题的关键.
 ,
,∴
 =(8,6)
=(8,6)∴
 =
= ;
;(2)因为
 ,
, ,当
,当 与
与 平行,
平行,则(k-4)×(8)-(4k-1)×6=0,解得:
 ,
,此时
 ,
,
=
 =
= =
=-
 (10,4)=-
(10,4)=- (
(  +2
+2  ),
),所以,
 与
与 反向.
反向.分析:(1)先根据条件求出向量
 的坐标,再利用向量的模的计算公式求出其模即可,
的坐标,再利用向量的模的计算公式求出其模即可,(2)当
 与
与 平行时,有(k-3)×(-4)-(2k+2)×10=0,解得
平行时,有(k-3)×(-4)-(2k+2)×10=0,解得 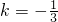 ,此时可得,
,此时可得,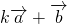 =-
=- (
(  -3
-3  ),故
),故  反向.
反向.点评:本题考查两个向量共线的条件和性质,两个向量坐标形式的运算,求出k值,是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
,
 ,
,  .
. ;
; 
 ,求
,求 的取值范围
的取值范围 .
. ;
; 与
与 平行,求
平行,求 的值;
的值;









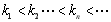






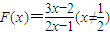
 ;
; .
.