题目内容
从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千克)与月储蓄yi(单位:千元)的数据资料,算得 i=80,
i=80, i=20,
i=20, iyi=184,
iyi=184,
 =720.
=720.
(1)求家庭的月储蓄y对月收入x的线性回归方程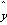 =
=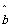 x+
x+ ;
;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.附:线性回归方程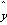 =
=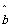 x+
x+ 中,
中,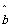 =
= ,
, =
= -
-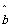
 ,
,
其中 ,
, 为样本平均值.
为样本平均值.
(1)由题意知n=10, =
=
 i=
i= =8,
=8, =
=
 i=
i= =2,
=2,
又
 -n
-n 2=720-10×82=80,
2=720-10×82=80, iyi-n
iyi-n
 =184-10×8×2=24,
=184-10×8×2=24,
由此得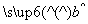 =
= =
= =0.3,
=0.3, =
= -
-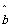
 =2-0.3×8=-0.4,
=2-0.3×8=-0.4,
故所求回归方程为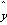 =0.3x-0.4.
=0.3x-0.4.
(2)由于变量y的值随x的值增加而增加(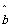 =0.3>0),故x与y之间是正相关.
=0.3>0),故x与y之间是正相关.
(3)将x=7代入回归方程可以预测该家庭的月储蓄为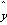 =0.3×7-0.4=1.7(千克).
=0.3×7-0.4=1.7(千克).

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
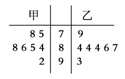 青年歌手大奖赛共有10名选手参赛,并请了7名评委.如图所示的茎叶图是7名评委给参加最后决赛的两位选手甲、乙评定的成绩,去掉一个最高分和一个最低分后,甲、乙选手剩余数据的平均成绩分别为________、________.
青年歌手大奖赛共有10名选手参赛,并请了7名评委.如图所示的茎叶图是7名评委给参加最后决赛的两位选手甲、乙评定的成绩,去掉一个最高分和一个最低分后,甲、乙选手剩余数据的平均成绩分别为________、________. =bx+a,那么下面说法不正确的是( )
=bx+a,那么下面说法不正确的是( ) ,
, )
)
 =bx+a和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差
=bx+a和各点(x1,y1),(x2,y2),…,(xn,yn)的偏差 yi-(bxi+a)]2是该坐标平面上所有直线与这些点的偏差中最小的直线.
yi-(bxi+a)]2是该坐标平面上所有直线与这些点的偏差中最小的直线. 的定义域为
的定义域为 ,则函数
,则函数 的定义域为 ( )
的定义域为 ( ) B.
B. C.
C.  D.
D.
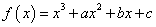 ,在定义域
,在定义域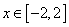 上表示的曲线过原点,且在
上表示的曲线过原点,且在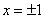 处的切线斜率均为
处的切线斜率均为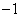 .有以下命题:
.有以下命题: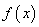 是奇函数;②若
是奇函数;②若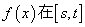 内递减,则
内递减,则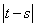 的最大值为4;③
的最大值为4;③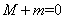 ;④若对
;④若对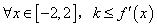 恒成立,则
恒成立,则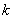 的最大值为2.其中正确命题的个数为 ( )
的最大值为2.其中正确命题的个数为 ( ) 的圆心坐标是( )
的圆心坐标是( ) B.
B. C.
C. D.
D.
 中,
中, 成等差数列,则
成等差数列,则 ( )
( )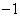 或3 D.1或27
或3 D.1或27