题目内容
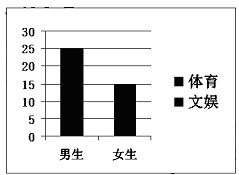
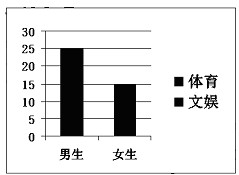对某班学生是更喜欢体育还是更喜欢文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．（I）根据图中数据，制作2×2列联表；
（II）若要从更喜欢体育的学生中随机选3人，组成体育爱好者交流小组，去外校参观学习，求小组中含女生人数的分布列和期望．
分析：（I）根据所给的二维条形图看出爱好体育和爱好文娱的学生数，得到列联表．
（II）由题意知ξ的取值为0，1，2，3，利用古典概型的概率公式求出随机变量取每一个值的概率，写出分布列，求出期望值．
（II）由题意知ξ的取值为0，1，2，3，利用古典概型的概率公式求出随机变量取每一个值的概率，写出分布列，求出期望值．
解答：解：（I）
（II）设小组中含女生人数为ξ，则ξ=0，1，2，3
P(ξ=0)=
=
，P(ξ=1)=
=
，
P(ξ=2)=
=
，P(ξ=3)=
=
所以所求的分布列为
所以女生人数为ξ的数学期望为Eξ=0×
+1×
+2×
+3×
=
（II）设小组中含女生人数为ξ，则ξ=0，1，2，3
P(ξ=0)=
| ||||
|
| 91 |
| 228 |
| ||||
|
| 35 |
| 76 |
P(ξ=2)=
| ||||
|
| 5 |
| 38 |
| ||||
|
| 1 |
| 114 |
所以所求的分布列为
所以女生人数为ξ的数学期望为Eξ=0×
| 91 |
| 228 |
| 35 |
| 76 |
| 5 |
| 38 |
| 1 |
| 114 |
| 3 |
| 4 |
点评：本题考查离散型随机变量的分布列和期望，考查古典概型的概率公式，考查独立重复试验的概率公式，考查利用概率与统计的知识解决实际问题．
练习册系列答案
53随堂测系列答案
相关题目
对某班学生是爱好体育还是爱好文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．（1）根据图中的数据，制作2×2列表；
（2）若要从更爱好文娱和从更爱好体育的学生中各选一人分别作文体活动的协调人，求选出的两人恰好是一男一女的概率；
（3）在多大的程度上可以认为性别与是否爱好体育有关系？
参考数据：
| P（K2≥k） | 0.5 | 0.4 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
对某班学生是爱好体育还是爱好文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．
（1）根据图中的数据，制作2×2列表；
（2）若要从更爱好文娱和从更爱好体育的学生中各选一人分别作文体活动的协调人，求选出的两人恰好是一男一女的概率；
（3）在多大的程度上可以认为性别与是否爱好体育有关系？
参考数据：
| P（K2≥k） | 0.5 | 0.4 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
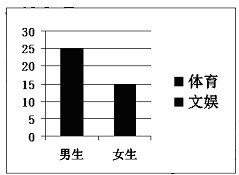对某班学生是更喜欢体育还是更喜欢文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．