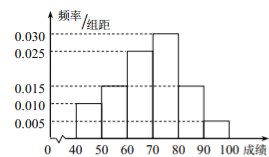
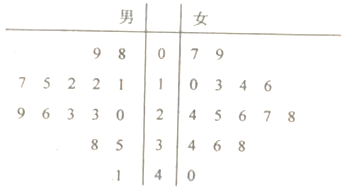
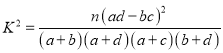题目内容
【题目】在直角坐标系
中，曲线
的参数方程为
为参数），以该直角坐标系的原点
为极点, 
轴的正半轴为极轴的极坐标系下，曲线
的方程为
.
（1）求曲线
的普通方程和曲线
的直角坐标方程；
（2）设曲线
和曲线
的交点为
、
，求
.
【答案】（Ⅰ）
．（Ⅱ）
．
【解析】试题分析：本题考查直角坐标系与极坐标之间的互化，考查学生利用坐标之间的转化求解.(1)消去参数
可得曲线
的普通方程，利用
,可把曲线
的极坐标方程转化为普通方程.（2）根据曲线
， 
的普通方程可判断出曲线
为直线，曲线
为圆，然后利用弦长公式
(其中
表示圆的半径， 
表示圆心到直线的距离)求值即可.
试题解析：（Ⅰ）曲线
的普通方程为
，曲线
的直角坐标方程为
． 3分
（Ⅱ）曲线
可化为
，表示圆心在
，半径
的圆，
则圆心到直线
的距离为
，所以
． 10分
练习册系列答案
相关题目
