题目内容
函数y=x-
的定义域是
| 3 | 2 |
(0,+∞)
(0,+∞)
.分析:根据幂函数的性质和分式的意义,被开方数大于0,可以求出x的范围即可.
解答:解:由于y=x-
=
,
得:x>0,
∴函数y=x-
的定义域是 (0,+∞).
故答案为:(0,+∞).
| 3 |
| 2 |
| 1 | ||
|
得:x>0,
∴函数y=x-
| 3 |
| 2 |
故答案为:(0,+∞).
点评:本题考查求函数的定义域问题,主要考查幂函数的概念、解析式、定义域、值域,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
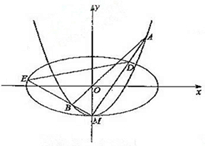 已知椭圆C1:
已知椭圆C1: