Question

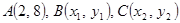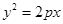(12分) 已知在抛物线上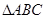，的重心与此抛物线的焦点F重合。

⑴ 写出该抛物线的标准方程和焦点F的坐标；

⑵ 求线段BC的中点M的坐标；

⑶ 求BC所在直线的方程。

 

Answer 1

【答案】

⑴方程为，焦点F的坐标为⑵⑶

【解析】

试题分析：⑴ 由点在抛物线上，有解得p =16，所以抛物线方程为，焦点F的坐标为。

⑵ 解法一：由于是的重心，设M是BC的中点，

所以，即有

设点M的坐标为，所以

解得，所以点M的坐标为

解法二：

∵M是BC的中点，

⑶ ∵点在抛物线上，

，又点在直线BC上

…12分

考点：抛物线方程及抛物线中的中点弦问题

点评：圆锥曲线的中点弦问题（直线与圆锥曲线相较于两点，涉及到弦的中点）采用点差法推理化简较容易，计算量小