题目内容
计算  在
在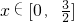 时函数的最大值和最小值.
时函数的最大值和最小值.
解:求导函数f′(x)=x2-3x+2=(x-1)(x-2)
令f′(x)>0,可得x<1或x>2;令f′(x)<0,可得1<x<2
∵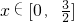
∴函数在[0,1]上单调增,在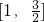 上单调减
上单调减
∴当x=1时,函数取得最大值f(1)=
∵
∴当x=0时,函数取得最小值f(0)=1
分析:先求导函数,再确定函数在定义域上的单调性,从而可求函数的最大值和最小值.
点评:本题重点考查函数的最值,考查导数知识的运用,解题的关键是利用导数确定函数在定义域上的单调性.
令f′(x)>0,可得x<1或x>2;令f′(x)<0,可得1<x<2
∵
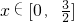
∴函数在[0,1]上单调增,在
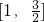 上单调减
上单调减∴当x=1时,函数取得最大值f(1)=

∵

∴当x=0时,函数取得最小值f(0)=1
分析:先求导函数,再确定函数在定义域上的单调性,从而可求函数的最大值和最小值.
点评:本题重点考查函数的最值,考查导数知识的运用,解题的关键是利用导数确定函数在定义域上的单调性.

练习册系列答案
相关题目
 在
在 时函数的最大值和最小值.
时函数的最大值和最小值.