Question

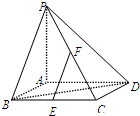（2013•崇明县二模）如图，已知四棱锥P-ABCD的底面ABCD为正方形，PA⊥平面ABCD，E、F分别是BC，PC的中点，
AB=2，AP=2．
（1）求三棱锥P-BCD的体积；
（2）求异面直线EF与PD所成角的大小．

Answer 1

分析：（1）根据题意，得PA是三棱锥P-BCD的高，求出△BCD的面积，再结合锥体体积公式，可得三棱锥P-BCD的体积；
（2）由三角形中位线定理，得EF∥PB，所以∠BPD或其补角为面直线EF与PD所成角，再通过计算得到△PBD是边长为2

2

的正三角形，得到异面直线EF与PD所成角的大小为60°．

解答：解：（1）∵PA⊥平面ABCD，∴PA是三棱锥P-BCD的高
又∵△BCD面积为S=

1

2

×2×2=2，
∴三棱锥P-BCD的体积V=

1

3

S_△BCD•PA=

1

3

×2×2=

4

3

（2）∵△PBC中，EF是中位线
∴EF∥PB，EF=

1

2

PB
可得∠BPD或其补角为面直线EF与PD所成角，
∵Rt△PAB中，PA=AB=2，∴PB=2

2

，同理可得PD=BD=2

2

因此△PBD是边长为2

2

的正三角形，∠BPD=60°
即异面直线EF与PD所成角的大小为60°．

点评：本题给出特殊四棱锥，求锥体的体积和异面直线所成角，着重考查了锥体体积公式和异面直线所成角求法等知识，属于基础题．