题目内容
如图1-25,已知C是线段AB上一点,△ACD与△BCE是两个等边三角形,AE交CD于G,BD交CE于H,求证:GH∥AB.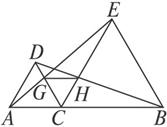
图1-25
证明:∵△ACD与△BCE是等边三角形,
∴∠ACD=∠CBE=60°.
∴DC∥BE.
∴
=
,
=
.
∵BC=BE,AC=DC,∴
=
.
∴
=
.
∴GH∥AB.
练习册系列答案
习题精选系列答案
相关题目
习题精选系列答案题目内容
如图1-25,已知C是线段AB上一点,△ACD与△BCE是两个等边三角形,AE交CD于G,BD交CE于H,求证:GH∥AB.
图1-25
证明:∵△ACD与△BCE是等边三角形,
∴∠ACD=∠CBE=60°.
∴DC∥BE.
∴=,=.
∵BC=BE,AC=DC,∴=.
∴=.
∴GH∥AB.
习题精选系列答案
（2013•宿迁一模）【选做题】本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
