题目内容
已知数列{an}中,a1=2,an+1= 。证明:数列{an}中任意连续四项之积为定值。
。证明:数列{an}中任意连续四项之积为定值。
 。证明:数列{an}中任意连续四项之积为定值。
。证明:数列{an}中任意连续四项之积为定值。证明:由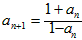
得: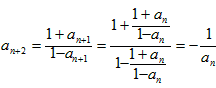
∴anan+2=-1,同理得an+1an+3=-1,
∴anan+1an+2an+3=1。
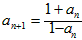
得:
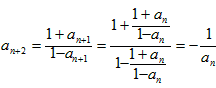
∴anan+2=-1,同理得an+1an+3=-1,
∴anan+1an+2an+3=1。

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|