题目内容
..(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分6分.
已知椭圆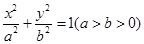 上有一个顶点到两个焦点之间的距离分别为
上有一个顶点到两个焦点之间的距离分别为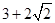 ,
,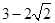 。
。
(1)求椭圆的方程;
(2)如果直线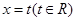 与椭圆相交于
与椭圆相交于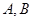 ,若
,若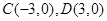 ,证明直线
,证明直线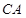 与直线
与直线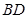 的交点
的交点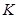 必在一条确定的双曲线上;
必在一条确定的双曲线上;
(3)过点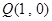 作直线
作直线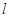 (与
(与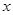 轴不垂直)与椭圆交于
轴不垂直)与椭圆交于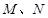 两点,与
两点,与 轴交于点
轴交于点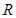 ,若
,若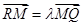 ,
,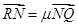 ,证明:
,证明: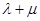 为定值。
为定值。
【答案】
解:(1)由已知
 ………………………3分
………………………3分
所以椭圆方程为 。………………………5分
。………………………5分
(2)依题意可设 ,且有
,且有
又
 ,将
,将 代入即得
代入即得
所以直线 与直线
与直线 的交点
的交点 必在双曲线
必在双曲线 上。……………………10分
上。……………………10分
(3)依题意,直线 的斜率存在,故可设直线
的斜率存在,故可设直线 的方程为
的方程为 ,……………11分
,……………11分
设 、
、 、
、 ,则
,则 两点坐标满足方程组
两点坐标满足方程组
消去 并整理,得
并整理,得 ,
,
所以 , ①
, ①
 , ② ……………………13分
, ② ……………………13分
因为 ,所以
,所以 ,
,
即 所以
所以 ,又
,又 与
与 轴不垂直,所以
轴不垂直,所以 ,
,
所以 ,同理
,同理 。 …………………………14分
。 …………………………14分
所以
 。
。
将①②代入上式可得 。 …………………………16分
。 …………………………16分
【解析】略

练习册系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在