题目内容
【题目】已知函数![]() ,曲线
,曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求实数![]() 的值;
的值;
(2)![]() 且
且![]() 时,证明:曲线
时,证明:曲线![]() 的图象恒在切线
的图象恒在切线![]() 的上方;
的上方;
(3)证明:不等式:![]() .
.
【答案】(1)![]() ,
,![]() ;(2)证明见解析;(3)证明见解析
;(2)证明见解析;(3)证明见解析
【解析】
(1)先表示出导数公式![]() ,结合导数的几何意义建立斜率的等量关系,再结合曲线过切点,即可求解;
,结合导数的几何意义建立斜率的等量关系,再结合曲线过切点,即可求解;
(2)由(1)的结论可将所求问题转化为当![]() 且
且![]() 时,
时,![]() ,构造函数
,构造函数![]() ,则
,则![]() ,无法判断正负,考虑再次求导:
,无法判断正负,考虑再次求导:![]() ,结合零点存在定理可判断
,结合零点存在定理可判断![]() 单增,必定存在
单增,必定存在![]() ,使得
,使得![]() ,倒推出
,倒推出![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,又结合端点值
单调递增,又结合端点值![]() ,
,![]() ,可得
,可得![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,![]() ,进而得证;
,进而得证;
(3)将所证不等式同除![]() 得
得![]() ,由(2)的结论进行放缩,可得
,由(2)的结论进行放缩,可得![]() ,即证
,即证![]() ,再次构造函数
,再次构造函数![]() ,结合导数求出函数最值,即可求证;
,结合导数求出函数最值,即可求证;
(1)![]() ,由曲线
,由曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() 知:
知:
![]() 解得
解得![]() ,
,![]() .
.
(2)由题意只需证:当![]() 且
且![]() 时,
时,![]() ;
;
设![]() ,则
,则![]() ,
,![]() ,易知
,易知![]() 在
在![]() 单调递增;且
单调递增;且![]() ,
,![]() ,∴必定存在
,∴必定存在![]() ,使得
,使得![]() ,则
,则![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,其中
单调递增,其中![]() ,
,
![]() ,即
,即![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,![]() ,即当
,即当![]() 且
且![]() 时,
时,
![]() 成立;
成立;
所以当![]() 且
且![]() 时,曲线
时,曲线![]() 的图象在切线
的图象在切线![]() 的上方.
的上方.
(3)要证:![]() ,只需证
,只需证![]() .
.
由(2)知![]() 时,
时,![]() .
.
故只需证![]() ,即证
,即证![]() ,
,
设![]() ,则
,则![]() ,易知
,易知![]() 在
在![]() 单调递减,
单调递减,
在![]() 单调递增,
单调递增,![]() ;
;
即不等式:![]() 成立.
成立.

 阅读快车系列答案
阅读快车系列答案【题目】2018年11月5日至10日,首届中国国际进口博览会在国家会展中心(上海)举行,吸引了58个“一带一路”沿线国家的超过1000多家企业参展,成为共建“一带一路”的又一个重要支撑.某企业为了参加这次盛会,提升行业竞争力,加大了科技投入.该企业连续6年来的科技投入![]() (百万元)与收益
(百万元)与收益![]() (百万元)的数据统计如下:
(百万元)的数据统计如下:
科技投入 | 2 | 4 | 6 | 8 | 10 | 12 |
收益 | 5.6 | 6.5 | 12.0 | 27.5 | 80.0 | 129.2 |
并根据数据绘制散点图如图所示:
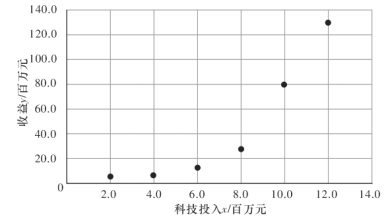
根据散点图的特点,甲认为样本点分布在指数曲线![]() 的周围,据此他对数据进行了一些初步处理.如下表:
的周围,据此他对数据进行了一些初步处理.如下表:
|
|
|
|
|
|
43.5 | 4.5 | 854.0 | 34.7 | 12730.4 | 70 |
其中![]() ,
,![]() .
.
(1)(i)请根据表中数据,建立![]() 关于
关于![]() 的回归方程(保留一位小数);
的回归方程(保留一位小数);
(ii)根据所建立的回归方程,若该企业想在下一年收益达到2亿,则科技投入的费用至少要多少?(其中![]() )
)
(2)乙认为样本点分布在二次曲线![]() 的周围,并计算得回归方程为
的周围,并计算得回归方程为![]() ,以及该回归模型的相关指数
,以及该回归模型的相关指数![]() ,试比较甲乙两人所建立的模型,谁的拟合效果更好.
,试比较甲乙两人所建立的模型,谁的拟合效果更好.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为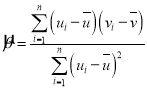 ,
,![]() ,相关指数:
,相关指数: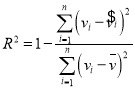 .
.
【题目】购买一辆某品牌新能源汽车,在行驶三年后,政府将给予适当金额的购车补贴.某调研机构对拟购买该品牌汽车的消费者,就购车补贴金额的心理预期值进行了抽样调查,其样本频率分布直方图如图所示
.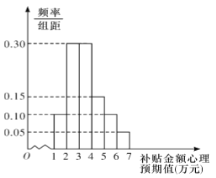
(1)估计拟购买该品牌汽车的消费群体对购车补贴金额的心理预期值的方差(同一组中的数据用该组区间的中点值作代表);
(2)将频率视为概率,从拟购买该品牌汽车的消费群体中随机抽取![]() 人,记对购车补贴金额的心理预期值高于
人,记对购车补贴金额的心理预期值高于![]() 万元的人数为
万元的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)统计最近![]() 个月该品牌汽车的市场销售量,得其频数分布表如下:
个月该品牌汽车的市场销售量,得其频数分布表如下:
月份 |
|
|
|
|
|
销售量(万辆) |
|
|
|
|
|
试预计该品牌汽车在![]() 年
年![]() 月份的销售量约为多少万辆?
月份的销售量约为多少万辆?
附:对于一组样本数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.