题目内容
(本题满分12分)
已知关于 的方程
的方程 :
: .
.
(1)当 为何值时,方程C表示圆。
为何值时,方程C表示圆。
(2)若圆C与直线 相交于M,N两点,且|MN|=
相交于M,N两点,且|MN|= ,求
,求 的值。
的值。
(3)在(2)条件下,是否存在直线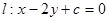 ,使得圆上有四点到直线
,使得圆上有四点到直线 的距离为
的距离为 ,若存在,求出
,若存在,求出 的范围,若不存在,说明理由。
的范围,若不存在,说明理由。
(1)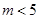 时方程C表示圆。(2)
时方程C表示圆。(2) ;(3)
;(3) 。
。
解析试题分析:(1)方程C可化为  ………………2分
………………2分
显然 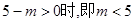 时方程C表示圆。………………4分
时方程C表示圆。………………4分
(2)圆的方程化为  圆心 C(1,2),半径
圆心 C(1,2),半径 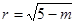 则圆心C(1,2)到直线l:x+2y-4=0的距离为
则圆心C(1,2)到直线l:x+2y-4=0的距离为 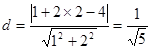 ………………6分
………………6分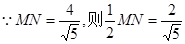 ,有
,有 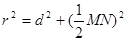
 得
得  …………8分
…………8分
(3)设存在这样的直线
圆心 C(1,2),半径 , 则圆心C(1,2)到直线
, 则圆心C(1,2)到直线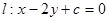 的距离为
的距离为
解得 ----------12分
----------12分
考点:本题主要考查圆的方程及点到直线的距离公式。
点评:典型题,涉及直线与圆的位置关系问题,要关注弦长、半径、圆心到直线的距离三者关系。

练习册系列答案
相关题目
 与圆C相切.
与圆C相切. 与圆C交于不同的两点A
与圆C交于不同的两点A 、B
、B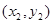 ,当
,当 时,求△AOB的面积.
时,求△AOB的面积. .
. )向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
 |PD|.
|PD|.
 ,求直线l的方程.
,求直线l的方程.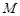 :
: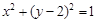 ,设点
,设点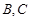 是直线
是直线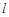 :
: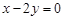 上的两点,它们的横坐标分别
上的两点,它们的横坐标分别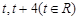 ,
,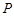 点的纵坐标为
点的纵坐标为 且点
且点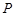 在线段
在线段 上,过
上,过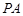 ,切点为
,切点为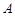
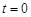 ,
,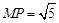 ,求直线
,求直线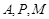 三点的圆的圆心是
三点的圆的圆心是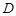 ,
,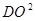 表示成
表示成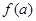 ,并写出定义域.
,并写出定义域.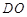 长的最小值
长的最小值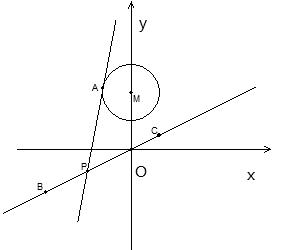
 ,圆
,圆
 和圆
和圆 的位置关系;
的位置关系; 的值.
的值. ,圆心M在二次曲线
,圆心M在二次曲线 上运动(1)若圆M与y轴相切,求圆M方程;(2) 已知圆M的圆心M在第一象限, 半径为
上运动(1)若圆M与y轴相切,求圆M方程;(2) 已知圆M的圆心M在第一象限, 半径为 ,动点
,动点 是圆M外一点,过点
是圆M外一点,过点 与圆M相切的切线的长为3,求动点
与圆M相切的切线的长为3,求动点 ,求
,求 的取值范围?
的取值范围?