题目内容
已知数列![]() 的通项公式为
的通项公式为![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]()
(I)求![]() 的通项公式;
的通项公式;
(II)在![]() 中是否存在使得
中是否存在使得![]() 是
是![]() 中的项,若存在,请写出满足题意的一项(不要求写出所有的项);若不存在,请说明理由.
中的项,若存在,请写出满足题意的一项(不要求写出所有的项);若不存在,请说明理由.
21世纪教育网
解:(I)当![]() 时,
时,![]() ………………………………………2分
………………………………………2分
当![]() 时,
时,![]()
两式相减得:![]() ,即:
,即:![]() …………………………………………6分
…………………………………………6分
故{![]() }为首项和公比均为
}为首项和公比均为![]() 的等比数列,
的等比数列,![]() ……………………………8分
……………………………8分
(II)设![]() 中第m项
中第m项![]() 满足题意,即
满足题意,即![]() ,即
,即![]()
所以![]()
![]() (其它形如
(其它形如![]() 的数均可)……………………12分
的数均可)……………………12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的通项公式为
的通项公式为 ,那么
,那么 是这个数列的( )
是这个数列的( ) ,则a3( )
,则a3( )



 的通项公式为
的通项公式为 ,设其前
,设其前 项和为
项和为 ,则使
,则使 成立的最小自然数
成立的最小自然数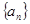 ,如果存在最小的一个常数
,如果存在最小的一个常数 ,使得对任意的正整数恒有
,使得对任意的正整数恒有 成立,则称数列
成立,则称数列 的周期数列。设
的周期数列。设 ,数列前
,数列前 项的和分别记为
项的和分别记为 ,则
,则 的通项公式为
的通项公式为 ,那么满足
,那么满足 的正整数
的正整数 =________
=________