题目内容
已知函数
(1)求函数f(x)的定义域;
(2)求函数f(x)的单调区间;
(3)求函数f(x)的最小值,并求取得最小值时x的值.
解:(1)∵函数 ,∴
,∴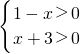 .解得-3<x<1,故函数的定义域为(-3,1).
.解得-3<x<1,故函数的定义域为(-3,1).
(2)∵ =
= .
.
令h(x)=(1-x)(x+3),则二次函数h(x)的图象开口向下,对称轴为x=-1.
在(-3,-1)上,h(x) 是增函数,故f(x)= 是减函数,故f(x)的减区间为(-3,-1).
是减函数,故f(x)的减区间为(-3,-1).
在[-1,1)上,h(x) 是减函数,故f(x)= 是增函数,故f(x)的增区间为[-1,1).
是增函数,故f(x)的增区间为[-1,1).
(3)利用函数f(x)的单调性可得,当x=-1时,函数f(x)取得最小值为-2.
分析:(1)由函数的解析式可得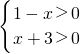 ,求出x的范围,即可求得函数的定义域.
,求出x的范围,即可求得函数的定义域.
(2)令h(x)=(1-x)(x+3),则f(x)= ,利用二次函数h(x)在(-3,1)上的单调性求得f(x)在(-3,1)上的单调性.
,利用二次函数h(x)在(-3,1)上的单调性求得f(x)在(-3,1)上的单调性.
(3)利用函数f(x)的单调性求出函数f(x)的最小值.
点评:本题主要考查对数型复合函数的性质以及应用,求函数的定义域、最值以及单调区间,二次函数性质的应用,
属于中档题.
 ,∴
,∴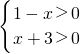 .解得-3<x<1,故函数的定义域为(-3,1).
.解得-3<x<1,故函数的定义域为(-3,1).(2)∵
 =
= .
.令h(x)=(1-x)(x+3),则二次函数h(x)的图象开口向下,对称轴为x=-1.
在(-3,-1)上,h(x) 是增函数,故f(x)=
 是减函数,故f(x)的减区间为(-3,-1).
是减函数,故f(x)的减区间为(-3,-1).在[-1,1)上,h(x) 是减函数,故f(x)=
 是增函数,故f(x)的增区间为[-1,1).
是增函数,故f(x)的增区间为[-1,1).(3)利用函数f(x)的单调性可得,当x=-1时,函数f(x)取得最小值为-2.
分析:(1)由函数的解析式可得
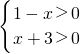 ,求出x的范围,即可求得函数的定义域.
,求出x的范围,即可求得函数的定义域.(2)令h(x)=(1-x)(x+3),则f(x)=
 ,利用二次函数h(x)在(-3,1)上的单调性求得f(x)在(-3,1)上的单调性.
,利用二次函数h(x)在(-3,1)上的单调性求得f(x)在(-3,1)上的单调性.(3)利用函数f(x)的单调性求出函数f(x)的最小值.
点评:本题主要考查对数型复合函数的性质以及应用,求函数的定义域、最值以及单调区间,二次函数性质的应用,
属于中档题.

练习册系列答案
相关题目



 的极值点;
的极值点; 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线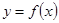 相切,求直线
相切,求直线 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)