题目内容
如图，在圆C：(x＋1)2＋y2＝25内有一点A(1，0)，Q为圆C上一点，AQ的垂直平分线与C，Q的连线交于点M，求点M的轨迹方程．
解 由题意知，点M在线段CQ上，
从而有|CQ|＝|MQ|＋|MC|.
又点M在AQ的垂直平分线上，则|MA|＝|MQ|，
∴|MA|＋|MC|＝|CQ|＝5.∵A(1，0)，C(－1，0)，
∴点M的轨迹是以(1，0)，(－1，0)为焦点的椭圆，
且2a＝5，故a＝
，c＝1，b2＝a2－c2＝
－1＝
.
故点M的轨迹方程为
＋
＝1.即
＋
＝1.
练习册系列答案
相关题目
中，如果存在非零常数T，使得
对于任意正整数n均成立，那么称数列
满足
，若
则当数列
。
，满足
,且在区间[0,2]上是增函数,则 
B. 
D. 
）内是增函数，则实数a的取值范围是（ ）
3 B. a
3
C. a<3 D. a>3
处的切线方程为____________
的一个焦点是
，那么实数
的值为（ ）
B 
C 
D 
是
的充要条件； ④
与
是等价的；
”是“
”成立的充分条件.
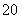＋2ax0＋2a≤0，若命题“p或q”是假命题，求a的取值范围．