题目内容
设a,b∈[0,1],则 的最小值为
的最小值为
- A.

- B.

- C.

- D.1
C
分析:通过构造函数 ,利用导数的方法求函数的最值,从而求出S的最小值.
,利用导数的方法求函数的最值,从而求出S的最小值.
解答:因为 =
= ≤1,
≤1,
当ab=0或ab=1时等号成立,
所以S的最大值为1.
令 ,
, ,
,
则
= .
.
设 ,
,
∴ ,
,
∴ ,
,
则
∴f(x)在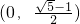 上是增函数,在
上是增函数,在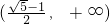 上是减函数,
上是减函数,
 时,
时,
所以f(x)有最大值 ,S的最小值为
,S的最小值为 ,
,
故选C.
点评:本题通过换元,构建函数,利用导数法求函数的最值,应注意这种思想方法在解题中的应用
分析:通过构造函数
 ,利用导数的方法求函数的最值,从而求出S的最小值.
,利用导数的方法求函数的最值,从而求出S的最小值.解答:因为
 =
= ≤1,
≤1,当ab=0或ab=1时等号成立,
所以S的最大值为1.
令
 ,
, ,
,则

=
 .
.设
 ,
,∴
 ,
,∴
 ,
,则

∴f(x)在
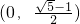 上是增函数,在
上是增函数,在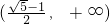 上是减函数,
上是减函数, 时,
时,所以f(x)有最大值
 ,S的最小值为
,S的最小值为 ,
,故选C.
点评:本题通过换元,构建函数,利用导数法求函数的最值,应注意这种思想方法在解题中的应用

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
设a,b∈[0,1],则S(a,b)=
+
+(1-a)(1-b)的最小值为( )
| a |
| 1+b |
| b |
| 1+a |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
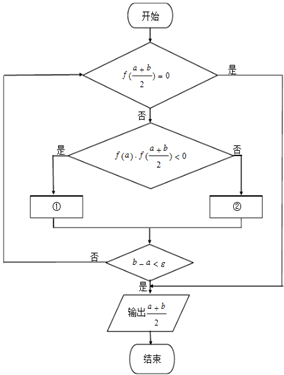 设区间[0,1]是方程f(x)=0的有解区间,用二分法求出方程f(x)=0在区间[0,1]上的一个近似解的流程图如图,设a,b∈[0,1],现要求精确度为ε,图中序号①,②处应填入的内容为( )
设区间[0,1]是方程f(x)=0的有解区间,用二分法求出方程f(x)=0在区间[0,1]上的一个近似解的流程图如图,设a,b∈[0,1],现要求精确度为ε,图中序号①,②处应填入的内容为( )A、a=
| ||||
B、b=
| ||||
C、a=
| ||||
D、b=
|