题目内容
已知棱长为l的正方体 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段 上,且
上,且 ,设面
,设面 面MPQ=
面MPQ= ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )

A. 面ABCD
面ABCD
B. AC
AC
C.面MEF与面MPQ不垂直
D.当x变化时, 不是定直线
不是定直线
 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段 上,且
上,且 ,设面
,设面 面MPQ=
面MPQ= ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )
A.
 面ABCD
面ABCDB.
 AC
ACC.面MEF与面MPQ不垂直
D.当x变化时,
 不是定直线
不是定直线D
试题分析:解:连结
 ,
, 交于点
交于点
 交于点
交于点
由正方体的性质知,

因为
 是
是 的中点,所以
的中点,所以
因为
 ,所以
,所以
所以
 ,所以
,所以 平面
平面 ,
, 平面
平面 ,
,由
 面MPQ=
面MPQ= ,
, 平面
平面 ,所以
,所以 ,而
,而 平面
平面 ,
, 平面
平面 ,
,所以,
 面ABCD ,所以选项A正确;
面ABCD ,所以选项A正确;由
 ,
, 得
得 而
而 ,所以
,所以 AC,所以选项B正确;
AC,所以选项B正确;连
 ,则
,则 而
而
所以,
 ,所以
,所以 平面
平面 ,过直线
,过直线 与平面
与平面 垂直的平面只能有一个,所以面MEF与面MPQ不垂直,所以选项C是正确的;
垂直的平面只能有一个,所以面MEF与面MPQ不垂直,所以选项C是正确的;因为
 ,
, 是定点,过直线外一点有且只有一条直线与已知直线平行,所以直线
是定点,过直线外一点有且只有一条直线与已知直线平行,所以直线 是唯一的,故选项D不正确.
是唯一的,故选项D不正确.
练习册系列答案
相关题目
 中,
中, ,
, ,
, ,
, ,
, ,E为CD上一点,
,E为CD上一点, ,
,

 ;
; 到平面
到平面 的距离。
的距离。 平面ABCD,E,F分别为MA,DC的中点,求证:
平面ABCD,E,F分别为MA,DC的中点,求证:
 ,Q为AD的中点.
,Q为AD的中点.

 平面PAD;
平面PAD;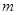 、
、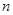 是两条直线,
是两条直线,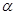 、
、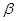 是两个平面,给出下列命题:①若
是两个平面,给出下列命题:①若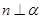 ,
,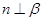 ,则
,则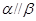 ;②若平面
;②若平面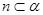 ,
,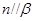 ,
,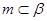 ,
,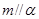 ,则
,则 个
个 个
个 个
个 个
个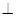 AB,则EF与CD所成的角为( ).
AB,则EF与CD所成的角为( ).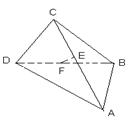
 B.
B. C.
C. D.
D.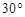





 是两条不同的直线,
是两条不同的直线,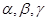 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: ,则
,则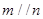 ;②若
;②若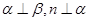 ,则
,则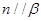 ;
;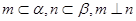 ,则
,则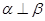 ; ④若
; ④若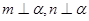 ,则
,则