题目内容
已知函数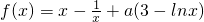 (a>0).
(a>0).
(Ⅰ)若a=1,求f(x)在(0,1]上的最大值;
(Ⅱ)若x∈(0,1),求f(x)的单调区间.
解:(Ⅰ)a=1时,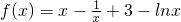 ,
,
则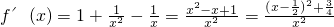 ,
,
当0<x≤1时,f'(x)>0,∴f(x)在(0,1]上单调递增,
∴f(x)在(0,1]上的最大值为f(1)=3.
(Ⅱ)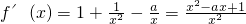 (0<x<1),判别式△=a2-4.
(0<x<1),判别式△=a2-4.
∵0<x<1,a>0,∴当△≤0时,
即0<a≤2时,x2-ax+1>0,因此,f'(x)>0,
此时,f(x)在(0,1)上单调递增,即f(x)只有增区间(0,1).
当△>0时,即a>2时,方程x2-ax+1=0有两个不等根,
设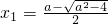 ,
,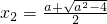 ,则0<x1<x2.当x变化时,f'(x),f(x)的变化如下:
,则0<x1<x2.当x变化时,f'(x),f(x)的变化如下:
 .
.
∵a>2,∴a-2>0.
而(a-2)2=a2-4a+4,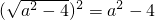 ,由a>2可得a2-4a+4<a2-4,∴
,由a>2可得a2-4a+4<a2-4,∴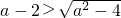 ,∴x1-1<0,∴x1<1.
,∴x1-1<0,∴x1<1.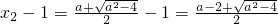 ,由a>2可得x2-1>0,∴x2>1.
,由a>2可得x2-1>0,∴x2>1.
因此,当a>2时,f(x)的增区间为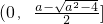 ,减区间为
,减区间为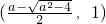 .
.
分析:(Ⅰ)先求出导函数极其单调性,利用单调性求出极值,再与端点函数值比较即可求f(x)在(0,1]上的最大值;
(Ⅱ)先求出导函数,以及单调区间的分界点,与区间端点进行比较即可求出x∈(0,1)时f(x)的单调区间.
点评:本题的第一问考查了利用导数求闭区间上函数的最值.求函数在闭区间[a,b]上的最大值与最小值是通过比较函数在(a,b)内所有极值与端点函数f(a),f(b) 比较而得到的.
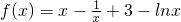 ,
,则
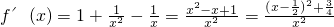 ,
,当0<x≤1时,f'(x)>0,∴f(x)在(0,1]上单调递增,
∴f(x)在(0,1]上的最大值为f(1)=3.
(Ⅱ)
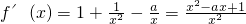 (0<x<1),判别式△=a2-4.
(0<x<1),判别式△=a2-4.∵0<x<1,a>0,∴当△≤0时,
即0<a≤2时,x2-ax+1>0,因此,f'(x)>0,
此时,f(x)在(0,1)上单调递增,即f(x)只有增区间(0,1).
当△>0时,即a>2时,方程x2-ax+1=0有两个不等根,
设
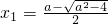 ,
,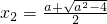 ,则0<x1<x2.当x变化时,f'(x),f(x)的变化如下:
,则0<x1<x2.当x变化时,f'(x),f(x)的变化如下:| x | (0,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
 .
.∵a>2,∴a-2>0.
而(a-2)2=a2-4a+4,
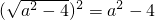 ,由a>2可得a2-4a+4<a2-4,∴
,由a>2可得a2-4a+4<a2-4,∴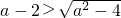 ,∴x1-1<0,∴x1<1.
,∴x1-1<0,∴x1<1.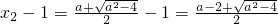 ,由a>2可得x2-1>0,∴x2>1.
,由a>2可得x2-1>0,∴x2>1.因此,当a>2时,f(x)的增区间为
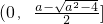 ,减区间为
,减区间为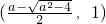 .
.分析:(Ⅰ)先求出导函数极其单调性,利用单调性求出极值,再与端点函数值比较即可求f(x)在(0,1]上的最大值;
(Ⅱ)先求出导函数,以及单调区间的分界点,与区间端点进行比较即可求出x∈(0,1)时f(x)的单调区间.
点评:本题的第一问考查了利用导数求闭区间上函数的最值.求函数在闭区间[a,b]上的最大值与最小值是通过比较函数在(a,b)内所有极值与端点函数f(a),f(b) 比较而得到的.

练习册系列答案
相关题目
 ,
, (a>0),若
(a>0),若 ,
, ,使得f(x1)= g(x2),则实数a的取值范围是( )
,使得f(x1)= g(x2),则实数a的取值范围是( ) (B)
(B)
 (C)
(C)
 (D)
(D)

 (a>0,且a≠1)
(a>0,且a≠1) (A>0,ω>0,x∈(-∞,+∞))的最小正周期为π,且
(A>0,ω>0,x∈(-∞,+∞))的最小正周期为π,且 ,则函数y=f(x)在
,则函数y=f(x)在 上的最小值是( )
上的最小值是( )


 其中a>0,e为自然对数的底数。
其中a>0,e为自然对数的底数。
 的单调区间;
的单调区间;