题目内容
已知四棱锥![]() 的底面
的底面![]() 为菱形,且
为菱形,且![]()
![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
(Ⅰ)求证:![]() 底面
底面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
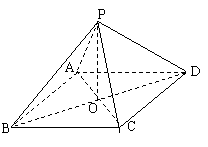 (Ⅲ)若
(Ⅲ)若![]() 是
是![]() 上的一点,且
上的一点,且![]() ,求
,求![]() 的值.
的值.
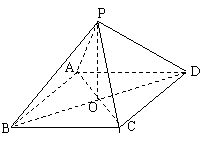 (Ⅰ)证明:因为
(Ⅰ)证明:因为![]() 为菱形,
为菱形,
所以![]() 为
为![]() 的中点……………………………1分
的中点……………………………1分
因为![]() ,
,
所以![]()
所以![]() 底面
底面 ![]() …………3分
…………3分
(Ⅱ)因为![]() 为菱形,所以
为菱形,所以![]()
建立如图所示空间直角坐标系
又![]()
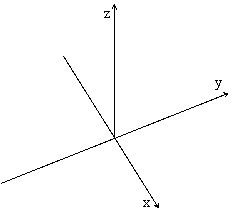 得
得![]() ……………………………4分
……………………………4分
所以![]()
![]() ,
,![]() ,
,![]() ………5分
………5分
设平面![]() 的法向量
的法向量![]()
有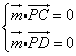
所以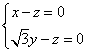 解得
解得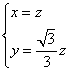
所以![]() ……………………………8分
……………………………8分
![]()
![]() ……………………………9分
……………………………9分
![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() …………………10分
…………………10分
(Ⅲ)因为点![]() 在
在![]() 上,所以
上,所以![]()
所以![]() ,
, ![]()
因为![]()
所以 ![]() , 得
, 得![]() 解得
解得![]()
所以![]() ……………………………14分
……………………………14分

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
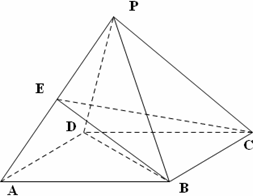

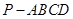 的底面
的底面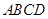 是边长为2的菱形,
是边长为2的菱形,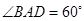 .已知
.已知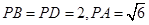 .
.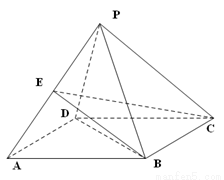
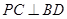
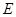 为
为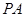 的中点,求三菱锥
的中点,求三菱锥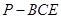 的体积.
的体积.