题目内容
解下列不等式
(1)x2-2x-3<0
(2)
≤0.
(1)x2-2x-3<0
(2)
| x2+2x-3 | -x2+x+6 |
分析:(1)求出方程x2-2x-3=0的两个根,即可求得不等式的解集;
(2)利用分式不等式的解法,将不等式等价转化为
,再进行化简,分别求解后取交集,即可得到不等式的解集.
(2)利用分式不等式的解法,将不等式等价转化为
|
解答:解:(1)∵x2-2x-3=0的解为x1=3或x2=-1,
∴不等式x2-2x-3<0变形为(x+1)(x-3)<0,
解得-1<x<3,
故不等式x2-2x-3<0的解集为{x|-1<x<3};
(2)不等式
≤0可以等价转化为
,
化简整理可得,
,即
,
解得x≤-3或-2<x≤1或x>3,
故不等式
≤0的解集为{x|x≤-3,或-2<x≤1,或x>3}.
∴不等式x2-2x-3<0变形为(x+1)(x-3)<0,
解得-1<x<3,
故不等式x2-2x-3<0的解集为{x|-1<x<3};
(2)不等式
| x2+2x-3 |
| -x2+x+6 |
|
化简整理可得,
|
|
解得x≤-3或-2<x≤1或x>3,
故不等式
| x2+2x-3 |
| -x2+x+6 |
点评:本题考查了一元二次不等式的解法,分式不等式的解法,高次不等式的解法.要求解一元二次不等式时,要注意与一元二次方程的联系,以及与二次函数之间的关系.求解不步骤是:判断最高次系数的正负,将负值转化为正值,确定一元二次方程的根的情况,利用二次函数的图象,写出不等式的解集.对于分式不等式,一般是“移项,通分”,将分式不等式转化为各个因式的正负问题.高次不等式一般选用“穿根法”进行求解,“穿根法”要注意先确定各因式的根,在数轴上按照从小到大标出来,确定各因式的系数为正值,根据“奇穿偶不穿”的原则,即可得到不等式的解集.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 >x-1;(2)
>x-1;(2)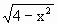 >-x-1.
>-x-1.