题目内容
根据下面各数列的前几项,写出数列的一个通项公式:
(1)3,5,9,17,33,…;
(2)
,
,
,
,
,…;
(3)2,-6,12,-20,30,-42,….
(1)3,5,9,17,33,…;
(2)
| 2 |
| 3 |
| 4 |
| 15 |
| 6 |
| 35 |
| 8 |
| 63 |
| 10 |
| 99 |
(3)2,-6,12,-20,30,-42,….
(1)联想数列2,4,8,16,32,,可知所求通项公式为an=2n+1.
(2)分别观察各项分子与分母的规律,分子为偶数列{2n};分母为1×3,3×5,5×7,7×9,
故所求通项公式为an=
.
(3)将数列变形为1×2,-2×3,3×4,-4×5,,于是可得已知数列的通项公式为an=(-1)n+1•n(n+1).
(2)分别观察各项分子与分母的规律,分子为偶数列{2n};分母为1×3,3×5,5×7,7×9,
故所求通项公式为an=
| 2n |
| (2n-1)(2n+1) |
(3)将数列变形为1×2,-2×3,3×4,-4×5,,于是可得已知数列的通项公式为an=(-1)n+1•n(n+1).

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 ,
,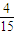 ,
,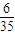 ,
,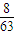 ,
,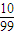 ,…;
,…;