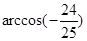题目内容
已知三点A(2,3),B(-1,-1),C(6,k),其中k为常数.若| |=|
|=| |,则
|,则 与
与 的夹角的余弦值为( )
的夹角的余弦值为( )A.-

B.0或

C.

D.0或-

【答案】分析:先求出 和
和 的坐标,由|
的坐标,由| |=|
|=| |求得 k=0,或 k=6.再分别利用两个向量夹角公式求出
|求得 k=0,或 k=6.再分别利用两个向量夹角公式求出 与
与 的夹角的余弦值.
的夹角的余弦值.
解答:解:由 =(-3,-4),
=(-3,-4), =(4,k-3),∴|
=(4,k-3),∴| |=|
|=| |,∴5=
|,∴5= ,解得 k=0,或 k=6.
,解得 k=0,或 k=6.
当 k=0时, =(4,-3),
=(4,-3), =-12+12=0,∴
=-12+12=0,∴ ,则
,则 与
与 的夹角的余弦值为0.
的夹角的余弦值为0.
当 k=6 时, =(4,3),
=(4,3), =-12-12=-24,cos<
=-12-12=-24,cos< ,
, >=
>= =
= =-
=- .
.
故选D.
点评:本题主要考查两个向量垂直的条件,两个向量坐标形式的运算,两个向量夹角公式的应用,体现了分类讨论的数学思想,属于中档题.
 和
和 的坐标,由|
的坐标,由| |=|
|=| |求得 k=0,或 k=6.再分别利用两个向量夹角公式求出
|求得 k=0,或 k=6.再分别利用两个向量夹角公式求出 与
与 的夹角的余弦值.
的夹角的余弦值.解答:解:由
 =(-3,-4),
=(-3,-4), =(4,k-3),∴|
=(4,k-3),∴| |=|
|=| |,∴5=
|,∴5= ,解得 k=0,或 k=6.
,解得 k=0,或 k=6.当 k=0时,
 =(4,-3),
=(4,-3), =-12+12=0,∴
=-12+12=0,∴ ,则
,则 与
与 的夹角的余弦值为0.
的夹角的余弦值为0.当 k=6 时,
 =(4,3),
=(4,3), =-12-12=-24,cos<
=-12-12=-24,cos< ,
, >=
>= =
= =-
=- .
.故选D.
点评:本题主要考查两个向量垂直的条件,两个向量坐标形式的运算,两个向量夹角公式的应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
已知三点A(2,3),B(-1,-1),C(6,k),其中k为常数.若|
|=|
|,则
与
的夹角为( )
| AB |
| AC |
| AB |
| AC |
A、arccos(-
| ||||
B、
| ||||
C、arccos
| ||||
D、
|
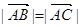 ,则向量
,则向量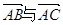 的夹角为(
)
的夹角为(
)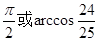 B.
B.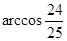
 D.
D.