Question

已知数列{a_n}中，a₁=1，a₂=3，且2a_n+1=a_n+2+a_n(n∈N₊).数列{b_n}的前n项和为S_n，其中b₁=,b_n+1=S_n(n∈N₊).

(1)求数列{a_n}和{b_n}的通项公式；

(2)若T_n=+…+,求T_n的表达式.

Answer 1

解:(1)∵2a_n+1=a_n+2+a_n,∴数列{a_n}是等差数列.

∴公差d=a₂-a₁=2.∴a_n=2n-1.

∵b_n+1=S_n,∴b_n=S_n-1(n≥2).

∴b_n+1-b_n=b_n,b_n+1=b_n.

又∵b₂=S₁=1,=≠,

∴数列{b_n}从第二项开始是等比数列.∴b_n=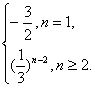

(2)∵n≥2时,=(2n-1)·3^n-2,

∴T_n=++…+=+3×3⁰+5×3¹+7×3²+…+(2n-1)×3^n-2.

∴3T_n=-2+3×3¹+5×3²+7×3³+…+(2n-1)×3^n-1.

错位相减并整理得T_n=+(n-1)×3^n-1.