题目内容
圆心在 轴上,且过两点A(1,4),B(3,2)的圆的方程为 .
轴上,且过两点A(1,4),B(3,2)的圆的方程为 .
 轴上,且过两点A(1,4),B(3,2)的圆的方程为 .
轴上,且过两点A(1,4),B(3,2)的圆的方程为 .
试题分析:因为圆心在
 轴上,所以设圆心坐标为(m,0),半径为r,则圆的方程为(x-m)2+y2=r2,因为圆经过两点A(1,4)、B(3,2),所以
轴上,所以设圆心坐标为(m,0),半径为r,则圆的方程为(x-m)2+y2=r2,因为圆经过两点A(1,4)、B(3,2),所以 ,解得:m=-1,r2=20,所以圆的方程为(x+1)2+y2=20。
,解得:m=-1,r2=20,所以圆的方程为(x+1)2+y2=20。点评:本题考查的重点是圆的标准方程的求法,解题的关键是根据设出的圆心坐标和半径表示出圆的方程,利用待定系数法求出圆心和半径。

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 ,直线L:
,直线L: 

 取什么实数,L与圆恒交于两点;
取什么实数,L与圆恒交于两点; 为圆
为圆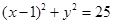 的弦AB的中点, 则直线AB的方程为 。
的弦AB的中点, 则直线AB的方程为 。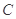 :
: 关于直线
关于直线 对称,则
对称,则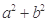 的最小值是( )
的最小值是( )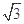


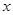 轴相切,圆心在直线
轴相切,圆心在直线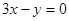 上,且被直线
上,且被直线 所截得的弦长为
所截得的弦长为 ,求此圆方程。
,求此圆方程。 ,直线
,直线 ,求与圆
,求与圆 相切,且与直线
相切,且与直线 垂直的直线方程。
垂直的直线方程。


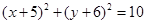
 ,则这个圆的方程是( )
,则这个圆的方程是( ) 的焦点。直线4x-3y-3=0与圆C相交于A,B两点,且|AB|=8,则圆C的方程为 。
的焦点。直线4x-3y-3=0与圆C相交于A,B两点,且|AB|=8,则圆C的方程为 。