题目内容
已知圆心在x轴上,半径是5且以A(5,4)为中点的弦长是2 ,则这个圆的方程是( )
,则这个圆的方程是( )
 ,则这个圆的方程是( )
,则这个圆的方程是( )| A.(x-3)2+y2=25 | B.(x-3)2+y2=25或(x-7)2+y2=25 |
| C.(x±3)2+y2=25 | D.(x+3)2+y2=25或(x+7)2+y2=25 |
B
试题分析:由圆心在x轴上,设圆心坐标为C(a,0),
又圆的半径r=5,弦BD长为2
 ,由垂径定理得到AC垂直于弦BD,∴|CA|2+(
,由垂径定理得到AC垂直于弦BD,∴|CA|2+( )2=52,又A(5,4),∴(5-a)2+42+5=25,解得:a=3或a=7,
)2=52,又A(5,4),∴(5-a)2+42+5=25,解得:a=3或a=7,则所求圆的方程为(x-3)2+y2=25或(x-7)2+y2=25.故选B
点评:解决该试题的关键是由圆心在x轴上,设出圆心C坐标为(a,0),由A为弦BD的中点,根据垂径定理得到AC垂直于BD,利用两点间的距离公式求出|AC|的长,再由圆的半径r及弦长的一半,根据勾股定理列出关于a的方程,求出方程的解得到a的值,确定出圆心的坐标,由圆心坐标及半径写出圆的标准方程即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的边
的边 所在直线的方程为
所在直线的方程为 ,
, 满足
满足 , 点
, 点 在
在 所在直线上且
所在直线上且 .
. 
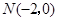 ,且与
,且与 的方程;
的方程; 斜率为
斜率为 的直线与曲线
的直线与曲线 两点,满足
两点,满足 ,求
,求 轴上,且过两点A(1,4),B(3,2)的圆的方程为 .
轴上,且过两点A(1,4),B(3,2)的圆的方程为 . 与圆
与圆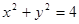 上任一点连线的中点轨迹方程是( )
上任一点连线的中点轨迹方程是( )


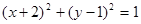
 始终平分圆
始终平分圆 的周长, 则a、b应满足的关系式是
的周长, 则a、b应满足的关系式是  0
0 0
0  0
0 0
0 平分的直线是( )
平分的直线是( )



 和
和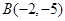 .
. 上,求圆的方程。
上,求圆的方程。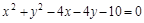 上的点到直线
上的点到直线 的最大距离是_________。
的最大距离是_________。