题目内容
已知函数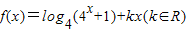
为偶函数．（Ⅰ） 求k的值；
（Ⅱ） 若方程
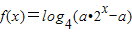有且只有一个实数解，求实数a的取值范围．
【答案】分析：（I）由f（x）为偶函数，可得f（-x）=f（x），代入整理可求k
（II）依题意知：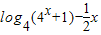
=
（*）
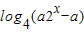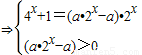令t=2x则*变为（1-a）t2+at+1=0只需其有一正根，根据二次方程的根的性质可求a的范围
解答：解：（I）因为f（x）为偶函数，
所以f（-x）=f（x）
∴
=
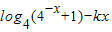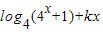
整理可得（2k+1）x=0
∴k=-
（II）依题意知：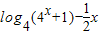
=
（*）
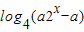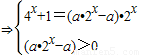
令t=2x则*变为（1-a）t2+at+1=0只需其有一正根．
（1）a=1，t=-1不合题意
（2）（*）式有一正一负根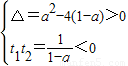
经验证满足a•2x-a＞0∴a＞1
（3）两相等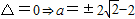
经验证a•2x-a＞0
∴
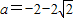
综上所述a＞1或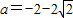
点评：本题主要考查了偶函数的定义的应用，二次方程的根的分布问题，要注意方程有一个正根与方程只要一个根是完全不同的概念．
（II）依题意知：
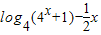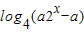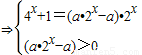=（*）令t=2x则*变为（1-a）t2+at+1=0只需其有一正根，根据二次方程的根的性质可求a的范围解答：解：（I）因为f（x）为偶函数，
所以f（-x）=f（x）
∴
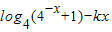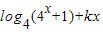
=整理可得（2k+1）x=0
∴k=-
（II）依题意知：
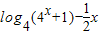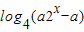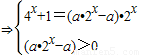
=（*）令t=2x则*变为（1-a）t2+at+1=0只需其有一正根．
（1）a=1，t=-1不合题意
（2）（*）式有一正一负根
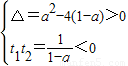
经验证满足a•2x-a＞0∴a＞1
（3）两相等
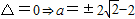
经验证a•2x-a＞0
∴
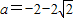
综上所述a＞1或
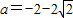
点评：本题主要考查了偶函数的定义的应用，二次方程的根的分布问题，要注意方程有一个正根与方程只要一个根是完全不同的概念．
练习册系列答案
相关题目
为偶函数高 考 资 源 网（
）其图像与直线y=2的某两个交点横坐标为
,若
的最小值为π，则（ ）
B 
C 
D 
为偶函数，且其图象上相邻两个最大值点之间的距离为
。
的表达式。（2）若
，求
的值。
为偶函数．
，判断λ与E的关系；
（m＞0，n＞0）时，若函数f（x）的值域为[2-3m，2-3n]，求m，n的值．
为偶函数，且函数y=f（x）图象的两相邻对称轴的距离为
．
个单位后，得到函数y=g（x）的图象，求g（x）的单调递减区间．
，使不等式f（x）＜m成立，求实数m的取值范围．
为偶函数，且其图象上相邻两对称轴之间的距离为
.
的表达式。
，求
的值.