题目内容
若存在过点(0,a)的直线与曲线y=x3和 都相切,则a的值为________.
都相切,则a的值为________.
-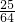 或-1
或-1
分析:已知点(1,0)不在曲线y=x3上,容易求出过点(1,0)的直线与曲线y=x3相切的切点的坐标,进而求出切线所在的方程;再利用切线与y=ax2+ x-9相切,只有一个公共点,两个方程联系,得到二元一次方程,利用判别式为0,解出a的值即可.
x-9相切,只有一个公共点,两个方程联系,得到二元一次方程,利用判别式为0,解出a的值即可.
解答:由y=x3?y'=3x2,
设曲线y=x3上任意一点(x0,x03)处的切线方程为y-x03=3x02(x-x0),
(1,0)代入方程得x0=0或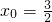
①当x0=0时,切线方程为y=0,则 ,
,
②当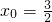 时,切线方程为
时,切线方程为  ,由
,由  ,
, ∴
∴ 或a=-1.
或a=-1.
故答案为:-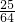 或-1.
或-1.
点评:本题主要考查了导数的几何意义,本题是直线与曲线联立的题,若出现形如y=ax2+bx+c的式子,注意应讨论a是否为0,考查了分类讨论的数学思想.
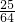 或-1
或-1分析:已知点(1,0)不在曲线y=x3上,容易求出过点(1,0)的直线与曲线y=x3相切的切点的坐标,进而求出切线所在的方程;再利用切线与y=ax2+
 x-9相切,只有一个公共点,两个方程联系,得到二元一次方程,利用判别式为0,解出a的值即可.
x-9相切,只有一个公共点,两个方程联系,得到二元一次方程,利用判别式为0,解出a的值即可.解答:由y=x3?y'=3x2,
设曲线y=x3上任意一点(x0,x03)处的切线方程为y-x03=3x02(x-x0),
(1,0)代入方程得x0=0或
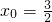
①当x0=0时,切线方程为y=0,则
 ,
,
②当
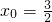 时,切线方程为
时,切线方程为  ,由
,由  ,
, ∴
∴ 或a=-1.
或a=-1.故答案为:-
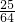 或-1.
或-1.点评:本题主要考查了导数的几何意义,本题是直线与曲线联立的题,若出现形如y=ax2+bx+c的式子,注意应讨论a是否为0,考查了分类讨论的数学思想.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 都相切,则a的值为 .
都相切,则a的值为 .