题目内容
设函数f(x)=3sin(2x+φ),φ∈(-π,0),y=f(x)图象的一条对称轴是直线
(1)求φ;
(2)求y=f(x)的减区间;
(3)当 时求y=f(x)的值域.
时求y=f(x)的值域.
解:(1)∵x= 是函数图象的一条对称轴,
是函数图象的一条对称轴,
∴
∴ ,
,
∵-π<?<0,
∴ .(4分)
.(4分)
(2)由(1)知?=- ,∴
,∴ ,
,
由题意得 ,则
,则 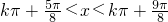
∴kπ+ ,k∈Z
,k∈Z
故函数函数f(x)的单调递减区间是
(3)∵ ,
,
∴
∴ [-1,
[-1, ]
]
∴

分析:(1)根据其图象的一条对称轴是直线 ,把这个自变量的值代入,写出关于所求的量的方程,结合-π<φ<0,求出φ的值.
,把这个自变量的值代入,写出关于所求的量的方程,结合-π<φ<0,求出φ的值.
(2)根据(1)求出函数的解析式,利用正弦函数的单调减区间,根据不等式的基本性质求出函数的单调增区间.
(3)根据所给的x的范围,写出 的范围,根据正弦曲线写出自变量的正弦值的范围,乘以3得到函数的值域.
的范围,根据正弦曲线写出自变量的正弦值的范围,乘以3得到函数的值域.
点评:本题考查三角函数的基本性质,函数的对称性,正弦函数的单调性,本题解题的关键是掌握基本函数的基本性质,本题是一个基础题.
 是函数图象的一条对称轴,
是函数图象的一条对称轴,∴

∴
 ,
,∵-π<?<0,
∴
 .(4分)
.(4分)(2)由(1)知?=-
 ,∴
,∴ ,
,由题意得
 ,则
,则 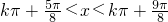
∴kπ+
 ,k∈Z
,k∈Z故函数函数f(x)的单调递减区间是

(3)∵
 ,
,∴

∴
 [-1,
[-1, ]
]∴


分析:(1)根据其图象的一条对称轴是直线
 ,把这个自变量的值代入,写出关于所求的量的方程,结合-π<φ<0,求出φ的值.
,把这个自变量的值代入,写出关于所求的量的方程,结合-π<φ<0,求出φ的值.(2)根据(1)求出函数的解析式,利用正弦函数的单调减区间,根据不等式的基本性质求出函数的单调增区间.
(3)根据所给的x的范围,写出
 的范围,根据正弦曲线写出自变量的正弦值的范围,乘以3得到函数的值域.
的范围,根据正弦曲线写出自变量的正弦值的范围,乘以3得到函数的值域.点评:本题考查三角函数的基本性质,函数的对称性,正弦函数的单调性,本题解题的关键是掌握基本函数的基本性质,本题是一个基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目

 时求y=f(x)的值域.
时求y=f(x)的值域. ),给出四个命题:①它的周期是2π;②它的图象关于直线x=
),给出四个命题:①它的周期是2π;②它的图象关于直线x= 成轴对称;③它的图象关于点(-
成轴对称;③它的图象关于点(- ,0)成中心对称;④它在区间[-
,0)成中心对称;④它在区间[- ,
, ]上是增函数.其中正确命题的序号是( )
]上是增函数.其中正确命题的序号是( )