题目内容
已知数列![]() 是等差数列,
是等差数列, ![]() ;数列
;数列![]() 的前n项和是
的前n项和是![]() ,且
,且![]() .
.
(Ⅰ) 求数列![]() 的通项公式;
的通项公式;
(Ⅱ) 求证:数列![]() 是等比数列;
是等比数列;
(Ⅲ) 记![]() ,求
,求![]() 的前n项和
的前n项和![]() .
.
已知数列![]() 是等差数列,
是等差数列, ![]() ;数列
;数列![]() 的前n项和是
的前n项和是![]() ,且
,且![]() .
.
(Ⅰ) 求数列![]() 的通项公式;
的通项公式;
(Ⅱ) 求证:数列![]() 是等比数列;
是等比数列;
(Ⅲ) 记![]() ,求
,求![]() 的前n项和
的前n项和![]() .
.
解:(1)设数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() .则有
.则有
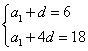 解得
解得![]()
所以数列![]() 的通项公式为
的通项公式为![]()
(2)当![]() 时,由
时,由![]() 及
及![]() 得
得![]()
当![]() 时, 由
时, 由![]() ①
①
知![]() ②
②
①-②得:
![]()
即:
![]()
因此,数列![]() 是等比数列,首项为
是等比数列,首项为![]() ,公比为
,公比为![]() 。
。
(3)由(2)知数列![]() 是等比数列,且首项为
是等比数列,且首项为![]() ,公比为
,公比为![]() 。
。
![]()
![]()
![]()
![]() ①
①
![]() ②
②
①-②得
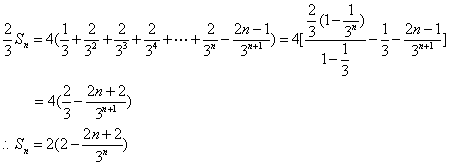

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是等差数列,若
是等差数列,若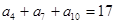 ,
, ,且
,且 ,则
,则 _________.
_________. 是等差数列,
是等差数列, ,则首项
,则首项 .
. 是等差数列,
是等差数列,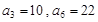 ,数列
,数列 的前n项和是
的前n项和是 ,且
,且 .
. 是等差数列,数列
是等差数列,数列 是等比数列,则
是等比数列,则 的值为 .
的值为 . }是等差数列,且满足:a1+a2+a3=6,a5=5;
}是等差数列,且满足:a1+a2+a3=6,a5=5; }满足:
}满足: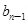 =
= (n≥2,n∈N﹡),b1=1.
(n≥2,n∈N﹡),b1=1. =
= (n∈N﹡),若{
(n∈N﹡),若{ ,求
,求