题目内容
下列命题:①命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”;
②若0<loga2<logb2,则a>b>1;
③已知a,b∈R*,2a+b=1,则
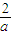 +
+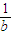 有最小值8;
有最小值8;④已知向量a=(1,2),b=(2,0),若向量λa+b与向量c=(1,-2)共线,则实数λ等于-1.
其中,正确命题的序号为 .
【答案】分析:①全称命题的否定是特称命题;
②底数大于0的对数函数,底数越大越靠近X轴;
③所求式子乘以1,而1用2a+b代换;
④向量λa+b的坐标表示可得,又由共线的充要条件x1y2-x2y1=0,得到关于实数λ的方程,解出即可.
解答:解:①命题“?x∈R,cosx>0”是全称命题,由于全称命题的否定是特称命题,故其否定是“?x∈R,cosx≤0”,则命题①正确;
②由于loga2>0,logb2>0,则a>1,b>1,又由loga2<logb2,则a>b>1,故命题②正确;
③由于a,b∈R*,2a+b=1,则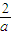 +
+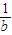 =
=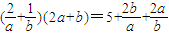
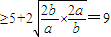 ,当且仅当
,当且仅当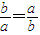 时,取等号
时,取等号
又由2a+b=1,则 时,取等号,故③错误;
时,取等号,故③错误;
④由于向量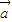 =(1,2),
=(1,2),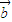 =(2,0),则向量
=(2,0),则向量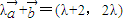 ,
,
又由向量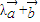 与向量
与向量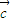 =(1,-2)共线,则-2(λ+2)-2λ=0,解得λ=-1,故④正确.
=(1,-2)共线,则-2(λ+2)-2λ=0,解得λ=-1,故④正确.
故答案为①②④.
点评:本题考查的知识点是,判断命题真假,我们需对四个结论逐一进行判断,方可得到正确的结论.
②底数大于0的对数函数,底数越大越靠近X轴;
③所求式子乘以1,而1用2a+b代换;
④向量λa+b的坐标表示可得,又由共线的充要条件x1y2-x2y1=0,得到关于实数λ的方程,解出即可.
解答:解:①命题“?x∈R,cosx>0”是全称命题,由于全称命题的否定是特称命题,故其否定是“?x∈R,cosx≤0”,则命题①正确;
②由于loga2>0,logb2>0,则a>1,b>1,又由loga2<logb2,则a>b>1,故命题②正确;
③由于a,b∈R*,2a+b=1,则
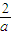 +
+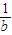 =
=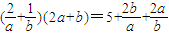
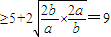 ,当且仅当
,当且仅当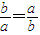 时,取等号
时,取等号又由2a+b=1,则
 时,取等号,故③错误;
时,取等号,故③错误;④由于向量
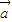 =(1,2),
=(1,2),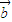 =(2,0),则向量
=(2,0),则向量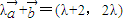 ,
,又由向量
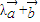 与向量
与向量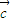 =(1,-2)共线,则-2(λ+2)-2λ=0,解得λ=-1,故④正确.
=(1,-2)共线,则-2(λ+2)-2λ=0,解得λ=-1,故④正确.故答案为①②④.
点评:本题考查的知识点是,判断命题真假,我们需对四个结论逐一进行判断,方可得到正确的结论.

练习册系列答案
相关题目