题目内容
已知函数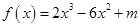 (
(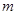 为常数)在
为常数)在 上有最大值3,那么此函数在
上有最大值3,那么此函数在 上的最小值为( )
上的最小值为( )
A.-29 B.-37 C.-5 D.-1
【答案】
B
【解析】
试题分析:因为 ,所以
,所以 ,由
,由 =0得,X=0,或x=2,计算f(-2)=m-40,f(0)
="m,f(2)" =m-8,所以m=3,故最小值为m-40=-37,选B。
=0得,X=0,或x=2,计算f(-2)=m-40,f(0)
="m,f(2)" =m-8,所以m=3,故最小值为m-40=-37,选B。
考点:本题主要考查导数计算,函数最值的概念及求法。
点评:典型题,利用导数求函数的最值,是高考常见题目。求极值的步骤:计算导数、求驻点、讨论驻点附近导数的正负、确定极值及端点函数值、比较确定最大值最小值。

练习册系列答案
相关题目
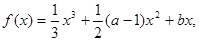 (
(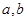 为常数)在
为常数)在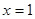 和
和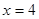 处取得极值,
处取得极值,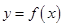 的解析式;
的解析式;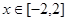 时,
时,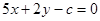 的下方,求实数
的下方,求实数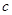 的取值范围.
的取值范围.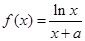 (
( 为常数)在点
为常数)在点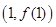 处
处 .
.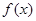 在区间
在区间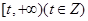 上存在极值,求
上存在极值,求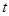 的最大值;
的最大值;