题目内容
11.(1)求经过两直线l1:2x-3y-3=0和l2:x+y+2=0的交点且与直线l:3x+y-1=0垂直的直线方程;(2)若两平行直线l1:2x+y-4=0和l2:y=-2x-k-2的距离不大于$\sqrt{5}$,求k的取值范围.
分析 (1)依题意,可求得两直线2x-3y-3=0和x+y+2=0的交点,利用所求直线与直线3x+y-1=0垂直可求得其斜率,从而可得其方程.
(2)直接利用平行线之间的距离列出不等式求解即可.
解答 解:(1)由两直线l1:2x-3y-3=0和l2:x+y+2=0得交点(-$\frac{3}{5}$,-$\frac{7}{5}$)
又直线3x+y-1=0斜率为-3,所求的直线与直线3x+y-1=0垂直,
所以所求直线的斜率为$\frac{1}{3}$,所求直线的方程为y+$\frac{7}{5}$=$\frac{1}{3}$(x+$\frac{3}{5}$),
化简得:5x-15y-18=0;
(2)两平行直线2x+y-4=0与y=-2x-m-2间的距离不大于$\sqrt{5}$,
可得:$\frac{|m+2+4|}{\sqrt{5}}≤\sqrt{5}$,解得-11≤x≤-1.
点评 本题考查平行线之间的距离的求法,考查计算能力,考查直线的一般式方程与直线的垂直关系,考查直线的点斜式方程,求得直线2x-3y-3=0和x+y+2=0的交点与斜率是关键,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
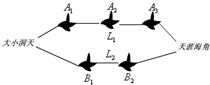 (理)“十一黄金周”期间三亚景区迎来了游客高峰期.游客小李从“大小洞天”到景区“天涯海角”景区有L1,L2两条路线(如图),路线L1上有A1,A2,A3三个风景点,各风景点遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1,B2两个风景点,各风景点遇到堵塞的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.
(理)“十一黄金周”期间三亚景区迎来了游客高峰期.游客小李从“大小洞天”到景区“天涯海角”景区有L1,L2两条路线(如图),路线L1上有A1,A2,A3三个风景点,各风景点遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1,B2两个风景点,各风景点遇到堵塞的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.