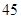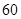题目内容
已知一个线性回归方程为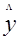
＝2x＋45，其中x的取值依次为1, 7, 5, 13, 19，
则
＝ ( )
| A．58.5 | B．46.5 | C．63 | D．75 |
C
解析试题分析：根据题意，由于线性回归方程为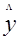＝2x＋45，则可知根据已知的数据得到
，由于回归方程过样本中心点，则可知当x=9,代入可知y=63,故可知=63，选C.
考点：线性回归方程
点评：本题考查线性回归方程的应用，本题解题的关键是知道样本中心点在线性回归方程上，本题是一个基础题．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案气象意义上从春季进入夏季的标志为：“连续5天的日平均温度均不低于22 0C”．现有甲、乙、丙三地连续5天的日平均温度的记录数据（记录数据都是正整数）：
① 甲地：5个数据的中位数为
，众数为
；
② 乙地：5个数据的中位数为
，总体均值为；
③ 丙地：5个数据中有一个数据是
，总体均值为
，总体方差为
；
则肯定进入夏季的地区有 ( )
| A．3个 | B．2个 | C．1个 | D．0个 |
下图是2013年某市举行的名师评选活动，七位评委为某位教师打出的分数的茎叶统计图，去掉一个最高分和一个最低分，所剩数据的平均数和方差分别为（ ）
| 7 | 9 | | | | |
| 8 | 4 | 4 | 6 | 4 | 7 |
| 9 | 3 | | | | |
B. 84，1.6
C. 85，1.6
D. 85，4
对变量x, y 有观测数据（
，
）（i=1,2,…，10），得散点图1；对变量u ，v 有观测数据（
，
）（i=1,2,…，10）,得散点图2. 由这两个散点图可以判断。 
图1 图2
| A．变量x 与y 正相关，u 与v 正相关 |
| B．变量x 与y 正相关，u 与v 负相关 |
| C．变量x 与y 负相关，u 与v 正相关 |
| D．变量x 与y 负相关，u 与v 负相关 |
某商品销售量y(件)与销售价格x(元/件)负相关，则其回归方程可能是( )
| A．y＝－10x＋200 | B．y＝10x＋200 |
| C．y＝－10x－200 | D．y＝10x－200 |
从甲乙两个城市分别随机抽取16台自动售货机，对其销售额进行统计，统计数据用茎叶图表示(如图所示)．设甲乙两组数据的平均数分别为
甲，乙，中位数分别为m甲，m乙，则( )．
| A．甲＜乙，m甲＞m乙 | B．甲＜乙，m甲＜m乙 |
| C．甲＞乙，m甲＞m乙 | D．甲＞乙，m甲＜m乙 |
某交警部门对城区上下班交通情况作抽样调查，上下班时间各抽取12辆机动车的行驶速度（单位：km/h）作为样本进行研究，做出样本的茎叶图，则上班、下班时间行驶速度的中位数分别是（ ）
| A．28 27.5 | B．28 28.5 |
| C．29 27.5 | D．29 28.5 |
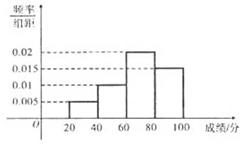
若低于60分的人数是15人，则该班的学生人数是( )
