题目内容
已知函数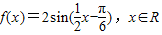
(1)求
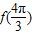 的值;
的值;(2)设
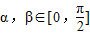 ,且α<β,
,且α<β,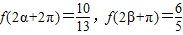 ,求sin(α-β)的值.
,求sin(α-β)的值.
【答案】分析:(1)直接令x=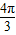 带入解析式求解即可
带入解析式求解即可
(2)角的变换为α-β=(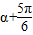 )-(
)-(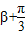 )-
)-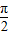 ,利用差角公式计算.注意开方时符号的确定.
,利用差角公式计算.注意开方时符号的确定.
解答:解:(1)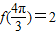 ------------------------------------(1分)
------------------------------------(1分)
f(2α+2π)=2sin(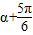 )=
)=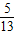 ,
,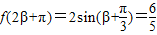
由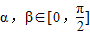 ,得出
,得出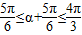 ,所以cos(
,所以cos(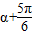 )=
)=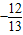
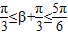 ,所以cos(
,所以cos(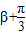 )=-
)=-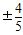
因为α-β=(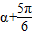 )-(
)-(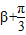 )-
)-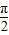
所以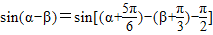 =
=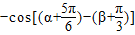 --------------------------------------------------(2分)
--------------------------------------------------(2分)
=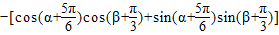 ---------------(1分)
---------------(1分)
当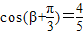 时,
时,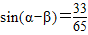 又因为
又因为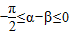 ,
,
所以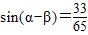 (舍去)-------------------------------------(1分)
(舍去)-------------------------------------(1分)
当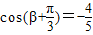 时,因为
时,因为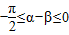 ,sin(α-β)<0
,sin(α-β)<0
所以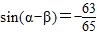 -----------------------------------------------------------------------------------(1分)
-----------------------------------------------------------------------------------(1分)
(另外可以这样限角 由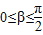 有
有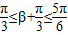
又因为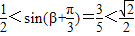 在
在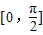 内
内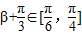
所以应该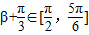 所以
所以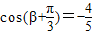 )
)
点评:本题考查和差角三角函数公式的应用.易错点在于开方时符号的确定.
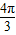 带入解析式求解即可
带入解析式求解即可(2)角的变换为α-β=(
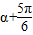 )-(
)-(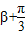 )-
)-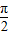 ,利用差角公式计算.注意开方时符号的确定.
,利用差角公式计算.注意开方时符号的确定.解答:解:(1)
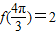 ------------------------------------(1分)
------------------------------------(1分)f(2α+2π)=2sin(
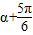 )=
)=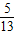 ,
,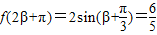
由
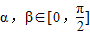 ,得出
,得出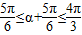 ,所以cos(
,所以cos(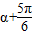 )=
)=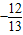
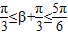 ,所以cos(
,所以cos(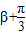 )=-
)=-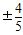
因为α-β=(
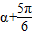 )-(
)-(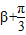 )-
)-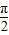
所以
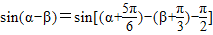 =
=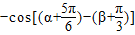 --------------------------------------------------(2分)
--------------------------------------------------(2分)=
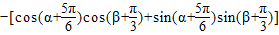 ---------------(1分)
---------------(1分)当
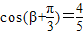 时,
时,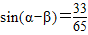 又因为
又因为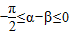 ,
,所以
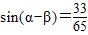 (舍去)-------------------------------------(1分)
(舍去)-------------------------------------(1分)当
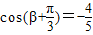 时,因为
时,因为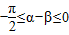 ,sin(α-β)<0
,sin(α-β)<0所以
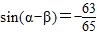 -----------------------------------------------------------------------------------(1分)
-----------------------------------------------------------------------------------(1分)(另外可以这样限角 由
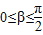 有
有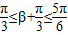
又因为
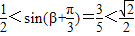 在
在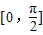 内
内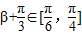
所以应该
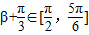 所以
所以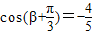 )
)点评:本题考查和差角三角函数公式的应用.易错点在于开方时符号的确定.

练习册系列答案
相关题目

 的值;
的值; ,求函数f(x)的值域.
,求函数f(x)的值域.
 的值;
的值; 成立的x的取值集合.
成立的x的取值集合.
 的值;
的值; 对称,且t∈(0,π),求t的值.
对称,且t∈(0,π),求t的值.
 的值;
的值; 成立的x的取值集合
成立的x的取值集合 .
. 的值;
的值; 的最大值及相应
的最大值及相应 的值.
的值.