题目内容
平面直角坐标系xOy中，已知点A（1，a）（a是常数）、B（2，4），直线x-y+1=0与线段AB相交，则a的取值范围是
（-∞，2]
（-∞，2]
．分析：由题意知，两点A（1，a）（a是常数）、B（2，4），分布在直线x-y+1=0的两侧，利用直线两侧的点的坐标代入直线的方程x-y+1=0中的左式，得到的结果为异号，得到不等式，解之即得a的取值范围．
解答：解：由题意得：
两点A（1，a）（a是常数）、B（2，4），分布在直线x-y+1=0的两侧，
∴（1-a+1）（2-4+1）≤0，
∴a∈（-∞，2]
故答案为：（-∞，2]．
两点A（1，a）（a是常数）、B（2，4），分布在直线x-y+1=0的两侧，
∴（1-a+1）（2-4+1）≤0，
∴a∈（-∞，2]
故答案为：（-∞，2]．
点评：本小题主要考查二元一次不等式（组）与平面区域、点与直线的位置关系、不等式的解法等基础知识，考查运算求解能力，属于基础题．
练习册系列答案
相关题目
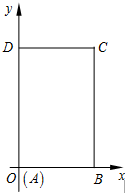如图，在平面直角坐标系xOy中，已知矩形ABCD的两边AB，CD分别落在x轴、y轴的正半轴上，且AB=2，AD=4，点A与坐标原点重合．现将矩形折叠，使点A落在线段DC上，若折痕所在的直线的斜率为k，试写出折痕所在直线的方程及k的范围．