题目内容
已知椭圆
（a＞b＞0）的左、右焦点分别为F1，F2，A为椭圆短轴的一个顶点，且△AF1F2是直角三角形，椭圆上任一点P到左焦点F1的距离的最大值为
（1）求椭圆C的方程；
（2）与两坐标轴都不垂直的直线l：y=kx+m（m＞0）交椭圆C于E，F两点，且以线段EF为直径的圆恒过坐标原点，当△OEF面积的最大值时，求直线l的方程．
【答案】分析：（1）由题意得，b=c，，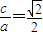
，
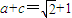，解方程求出a、b、c的值，即得椭圆的方程．
（2）把直线方程代入椭圆的方程，利用根与系数的关系以及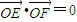
，即x1x2+y1y2=0，求得
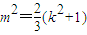，代入△OEF的面积公式换元后使用基本不等式可得面积S的最大值及此时的m、k的值．
解答：解：（1）由题意得，b=c，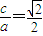
，
，
∴
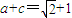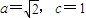，则b=1． 所以，椭圆的方程为
．
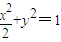（2）设E（x1，y1），F（x2，y2），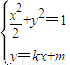
，
联立得（1+2k2）x2+4mkx+2m2-2=0，∴△=8（2k2+1-m2）＞0，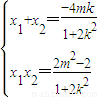
，
又以线段EF为直径的圆恒过坐标原点，所以，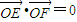
，
即x1x2+y1y2=0，代入得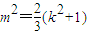
，
△OEF的面积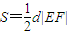
=
，
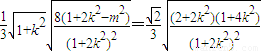设t=1+2k2＞1，则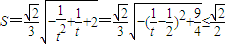
，
当t=2，即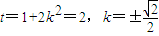
时，面积S取得最大值
，
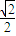此时，m=1，所以，直线方程为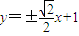
．
点评：本题考查用待定系数法求椭圆的方程，一元二次方程根与系数的关系，以及基本不等式的应用．
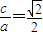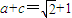，，解方程求出a、b、c的值，即得椭圆的方程．（2）把直线方程代入椭圆的方程，利用根与系数的关系以及
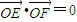，即x1x2+y1y2=0，求得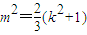，代入△OEF的面积公式换元后使用基本不等式可得面积S的最大值及此时的m、k的值．解答：解：（1）由题意得，b=c，
，，∴
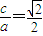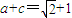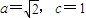，则b=1． 所以，椭圆的方程为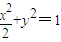．（2）设E（x1，y1），F（x2，y2），
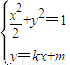，联立得（1+2k2）x2+4mkx+2m2-2=0，∴△=8（2k2+1-m2）＞0，
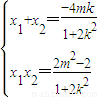，又以线段EF为直径的圆恒过坐标原点，所以，
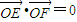，即x1x2+y1y2=0，代入得
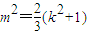，△OEF的面积
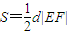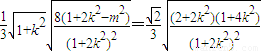=，设t=1+2k2＞1，则
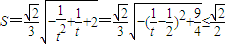，当t=2，即
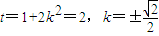时，面积S取得最大值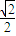，此时，m=1，所以，直线方程为
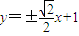．点评：本题考查用待定系数法求椭圆的方程，一元二次方程根与系数的关系，以及基本不等式的应用．
练习册系列答案
相关题目
=1(a＞b＞0)与双曲线
=1(m＞0,n＞0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是( )
B.
C.
D.
=1(a＞b＞0)，F1、F2分别为椭圆的左、右焦点，A为椭圆的上的顶点，直线AF2交椭圆于另 一点B.
＝2
，
·
＝
，求椭圆的方程．
（a>b>0）,点
在椭圆上。
（a＞b＞0）的焦距为4，且与椭圆
有相同的离心率，斜率为k的直线l经过点M（0，1），与椭圆C交于不同两点A、B．
分)
（a＞b＞0）的离心率
，焦距是函数
的零点.
与椭圆交于
、
两点,
，求k的值．