题目内容
已知方程
有两个不同的实数根x1，x2，则有（ ）A．x1x2＞1
B．x1x2＜0
C．0＜x1x2＜1
D．x1x2=1
【答案】分析：分别作出函数y=
和 y=|lgx|的图象如图，不妨设 0＜x1＜1＜x2，则|lgx1|＞|lgx2|，即-lgx1＜lgx2，化简可得结论．
解答：
解：分别作出函数y=
和 y=|lgx|的图象如图，不妨设 0＜x1＜1＜x2，则|lgx1|＞|lgx2|，
∴-lgx1＜lgx2，即 lgx1+lg x2＜0，∴0＜x1x2 ＜1，
故选C．
点评：本题主要考查函数的零点的判定定理的应用，体现了转化、数形结合的数学思想，属于基础题．
和 y=|lgx|的图象如图，不妨设 0＜x1＜1＜x2，则|lgx1|＞|lgx2|，即-lgx1＜lgx2，化简可得结论．解答：
解：分别作出函数y=和 y=|lgx|的图象如图，不妨设 0＜x1＜1＜x2，则|lgx1|＞|lgx2|，∴-lgx1＜lgx2，即 lgx1+lg x2＜0，∴0＜x1x2 ＜1，
故选C．
点评：本题主要考查函数的零点的判定定理的应用，体现了转化、数形结合的数学思想，属于基础题．
练习册系列答案
相关题目
有两个不同的零点
，且方程
有两个不同的实根
.若把这四个数按从小到大排列构成等差数列，则实数
的值为
B．
C．
D．
在一个周期内的图像下图所示。
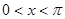，且方程
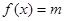有两个不同的实数根，求实数m的取值范围和这两个根的和。
有两个不同的实数根x1，x2，则有
有两个不同的实数根x1，x2，则有（ ）