题目内容
已知数列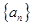 :
: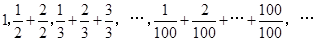
(1)观察规律,写出数列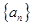 的通项公式,它是个什么数列?
的通项公式,它是个什么数列?
(2)若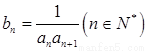 ,设
,设 ,求
,求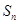 。
。
(3)设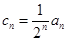 ,
,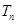 为数列
为数列 的前
的前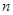 项和,求
项和,求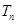 。
。
【答案】
(1) 为等差数列,公差
为等差数列,公差
(2)
(3)
【解析】
试题分析:解:①由条件,
∴ ;∴
;∴
故 为等差数列,公差
为等差数列,公差
②
又知
∴

③

相减,得


所以
考点:数列的求和
点评:主要是考查了裂项求和和错位相减法求和的综合运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列an=(1-2a)n,若
an存在,则a的范围是( )
| lim |
| n→∞ |
| A、[0,1] | ||||
B、[0,
| ||||
| C、[0,1) | ||||
| D、(0,1) |
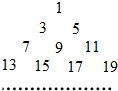 (2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是
(2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是