题目内容
求证: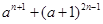 能被
能被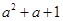 整除(其中
整除(其中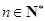 ).
).
【答案】
见解析
【解析】
试题分析:证明:(1)当 时,
时, 能被
能被 整除,即当
整除,即当 时原命题成立.
时原命题成立.
(2)假设 时,
时, 能被
能被 整除.
整除.
则当 时,
时,

 .
.
由归纳假设及 能被
能被 整除可知,
整除可知, 也能被
也能被 整除,即
整除,即 命题也成立.
命题也成立.
根据(1)和(2)可知,对于任意的 ,原命题成立.
,原命题成立.
考点:本题主要考查数学归纳法的概念及方法步骤。
点评:典型题,注意观察式子的结构特点,从K到k+1的变化进行有目的的“配凑”变形。

练习册系列答案
相关题目

