题目内容
定义函数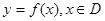 (
(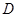 为定义域)图像上的点到坐标原点的距离为函数的
为定义域)图像上的点到坐标原点的距离为函数的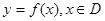 的模.若模存在最大值,则称之为函数
的模.若模存在最大值,则称之为函数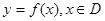 的长距;若模存在最小值,则称之为函数
的长距;若模存在最小值,则称之为函数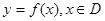 的短距.
的短距.
(1)分别判断函数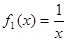 与
与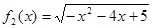 是否存在长距与短距,若存在,请求出;
是否存在长距与短距,若存在,请求出;
(2)求证:指数函数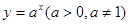 的短距小于1;
的短距小于1;
(3)对于任意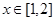 是否存在实数
是否存在实数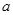 ,使得函数
,使得函数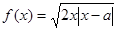 的短距不小于2,若存在,请求出
的短距不小于2,若存在,请求出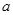 的取值范围;不存在,则说明理由?
的取值范围;不存在,则说明理由?
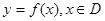 (
(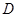 为定义域)图像上的点到坐标原点的距离为函数的
为定义域)图像上的点到坐标原点的距离为函数的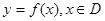 的模.若模存在最大值,则称之为函数
的模.若模存在最大值,则称之为函数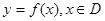 的长距;若模存在最小值,则称之为函数
的长距;若模存在最小值,则称之为函数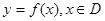 的短距.
的短距.(1)分别判断函数
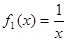 与
与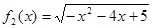 是否存在长距与短距,若存在,请求出;
是否存在长距与短距,若存在,请求出;(2)求证:指数函数
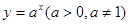 的短距小于1;
的短距小于1;(3)对于任意
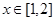 是否存在实数
是否存在实数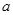 ,使得函数
,使得函数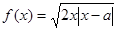 的短距不小于2,若存在,请求出
的短距不小于2,若存在,请求出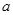 的取值范围;不存在,则说明理由?
的取值范围;不存在,则说明理由?(1)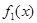 短距为
短距为 ,长距不存在,
,长距不存在, 短距为
短距为 ,长距为5;(2)证明见解析;(3)
,长距为5;(2)证明见解析;(3) .
.
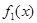 短距为
短距为 ,长距不存在,
,长距不存在, 短距为
短距为 ,长距为5;(2)证明见解析;(3)
,长距为5;(2)证明见解析;(3) .
.试题分析:本题属于新定义概念,问题的实质是求函数
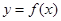 图象上的点到原点的距离的最大值和最小值(如有的话),正面讨论时我们把距离表示为
图象上的点到原点的距离的最大值和最小值(如有的话),正面讨论时我们把距离表示为 的函数.(1)对
的函数.(1)对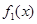 ,
,
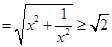 (当且仅当
(当且仅当 时等号成立),因此存在短距为
时等号成立),因此存在短距为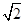 ,不存在长距,对
,不存在长距,对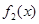 ,
,
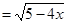 ,
, ,即有最大值也有最小值,因此短距和长距都有;(2)对函数
,即有最大值也有最小值,因此短距和长距都有;(2)对函数 ,
, ,由于
,由于 ,因此短距不大于1,令
,因此短距不大于1,令 ,则有
,则有 ,故当
,故当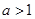 时,存在
时,存在 使得
使得
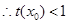 ,当
,当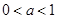 时,存在
时,存在 使得
使得
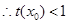 ,即证;(3)记
,即证;(3)记 ,按题意条件,则有不等式
,按题意条件,则有不等式 对
对 恒成立,这类不等式恒成立求参数取值范围问题,我们可采取分离参数法,转化为求函数的最值,按
恒成立,这类不等式恒成立求参数取值范围问题,我们可采取分离参数法,转化为求函数的最值,按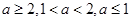 分别讨论,由此可求得
分别讨论,由此可求得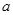 的范围.
的范围.(1)设
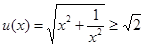 (当且仅当
(当且仅当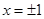 取得等号)+2分
取得等号)+2分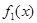 短距为
短距为 ,长距不存在。 +4分
,长距不存在。 +4分(2)设
 +6分
+6分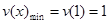
 +8分
+8分 短距为
短距为 ,长距为5。 +9分
,长距为5。 +9分(3)设

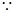 函数
函数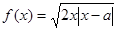 的短距不小于2
的短距不小于2即
 对于
对于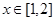 始终成立:+10分
始终成立:+10分当
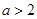 时:
时: 对于
对于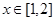 始终成立
始终成立 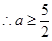 +12分
+12分当
 时:取
时:取 即可知显然不成立 +13分
即可知显然不成立 +13分当
 时:
时: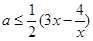 对于
对于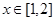 始终成立
始终成立  +15分
+15分综上
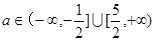 +16分
+16分
练习册系列答案
相关题目
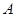 表示值域为R的函数组成的集合,
表示值域为R的函数组成的集合,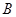 表示具有如下性质的函数
表示具有如下性质的函数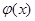 组成的集合:对于函数
组成的集合:对于函数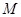 ,使得函数
,使得函数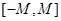 .例如,当
.例如,当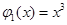 ,
,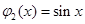 时,
时,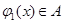 ,
,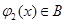 .现有如下命题:
.现有如下命题: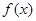 的定义域为
的定义域为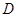 ,则“
,则“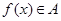 ”的充要条件是“
”的充要条件是“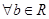 ,
,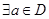 ,
,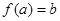 ”;
”;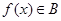 的充要条件是
的充要条件是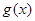 的定义域相同,且
的定义域相同,且 ,则
,则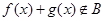 ;
;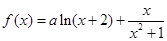 (
(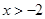 ,
,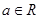 )有最大值,则
)有最大值,则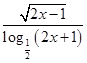 ,f(x)的定义域是________.
,f(x)的定义域是________.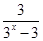 的值域为( )
的值域为( ) 的定义域是 .
的定义域是 .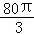 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
 的单调增区间为( )
的单调增区间为( )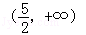

 则
则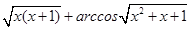 的值为
的值为