题目内容
如果n=∫-22(sinx+1)dx,则(1+2x)(1-x)n展开式中x2项的系数为 .
【答案】分析:由定积分的计算,可得n的值,进而分析在(1+2x)(1-x)n展开式中产生x2项的情况,分2种情况讨论,计算可得答案.
解答:解:根据题意,n=∫-22(sinx+1)dx=2-cos2-(-2)+cos(-2)=4,
则(1+2x)(1-x)4中,x2项产生有2种情况,
①(1+2x)中出常数项,(1-x)4中出x2项,
②(1+2x)与(1-x)4中,都出x项;
则其展开式中x2的系数为1×C42(-1)2+2×C43(-1)=-2;
故答案为:-2.
点评:本题考查二项式定理的运用,解题时关键在于对(1+2x)(1-x)n展开式中如何产生x2项的几种情况的分析讨论.
解答:解:根据题意,n=∫-22(sinx+1)dx=2-cos2-(-2)+cos(-2)=4,
则(1+2x)(1-x)4中,x2项产生有2种情况,
①(1+2x)中出常数项,(1-x)4中出x2项,
②(1+2x)与(1-x)4中,都出x项;
则其展开式中x2的系数为1×C42(-1)2+2×C43(-1)=-2;
故答案为:-2.
点评:本题考查二项式定理的运用,解题时关键在于对(1+2x)(1-x)n展开式中如何产生x2项的几种情况的分析讨论.

练习册系列答案
相关题目
对于函数f(x),如果有限集合S满足:①S⊆N*;②当x∈S时,f(x)∈S,则称集合S是函数f(x)的生成集.例如f(x)=4-x,那么集合S1={2},S2={1,3},S3={1,2,3}都是f(x)的生成集,对于f(x)=
(x>2,a,b∈R,若f(x)是减函数,S是f(x)的生成集,则S不可能是( )
| ax+b |
| x-2 |
| A、{3,4,5,6,8,14} |
| B、{3,4,6,10,18} |
| C、{3,5,6,7,10,16} |
| D、{3,4,6,7,12,22} |
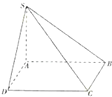 (2011•许昌三模)已知四棱锥S-ABCD中,AB=BC=CD=DA=SA=2,底面ABCD是正方形,SD=SB=
(2011•许昌三模)已知四棱锥S-ABCD中,AB=BC=CD=DA=SA=2,底面ABCD是正方形,SD=SB=