题目内容
(本题满分10分) 在直角坐标系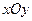 中,以
中,以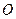 极点,
极点,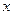 轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为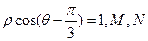 分别为
分别为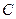 与
与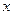 轴,
轴,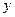 轴的交点
轴的交点
(1)写出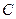 的直角坐标方程,并求出
的直角坐标方程,并求出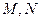 的极坐标
的极坐标
(2)设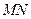 的中点为
的中点为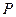 ,求直线
,求直线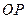 的极坐标方程
的极坐标方程
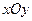 中,以
中,以 极点,
极点, 轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为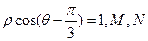 分别为
分别为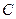 与
与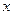 轴,
轴,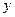 轴的交点
轴的交点(1)写出
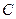 的直角坐标方程,并求出
的直角坐标方程,并求出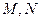 的极坐标
的极坐标(2)设
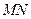 的中点为
的中点为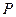 ,求直线
,求直线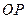 的极坐标方程
的极坐标方程(1)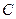 直角坐标方程为
直角坐标方程为 ,即
,即 ,
, ;
; 时,
时, ,所以
,所以 。
。
(2)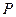 点的直角坐标为
点的直角坐标为 ,则
,则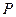 点的极坐标为
点的极坐标为 ,
,
所以直线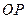 的极坐标方程为
的极坐标方程为 ,
,
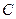 直角坐标方程为
直角坐标方程为 ,即
,即 ,
, ;
; 时,
时, ,所以
,所以 。
。(2)
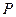 点的直角坐标为
点的直角坐标为 ,则
,则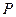 点的极坐标为
点的极坐标为 ,
,所以直线
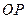 的极坐标方程为
的极坐标方程为 ,
,
解:(1)由 得
得 ,
,
从而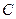 直角坐标方程为
直角坐标方程为 ,即
,即
 时,
时, ,所以
,所以 ;
; 时,
时, ,所以
,所以


 5分
5分
(2) 点的直角坐标为
点的直角坐标为 ,
, 点的直角坐标为
点的直角坐标为 ,
,
所以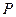 点的直角坐标为
点的直角坐标为 ,则
,则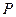 点的极坐标为
点的极坐标为 ,
,
所以直线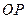 的极坐标方程为
的极坐标方程为 ,
,






 10分
10分
 得
得 ,
,从而
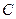 直角坐标方程为
直角坐标方程为 ,即
,即
 时,
时, ,所以
,所以 ;
; 时,
时, ,所以
,所以


 5分
5分(2)
 点的直角坐标为
点的直角坐标为 ,
, 点的直角坐标为
点的直角坐标为 ,
,所以
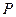 点的直角坐标为
点的直角坐标为 ,则
,则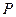 点的极坐标为
点的极坐标为 ,
,所以直线
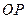 的极坐标方程为
的极坐标方程为 ,
,






 10分
10分
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
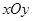 中,已知曲线
中,已知曲线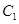 :
: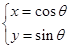 (
(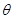 为参数),将
为参数),将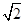 和
和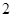 倍后得到曲线
倍后得到曲线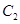 .以平面直角坐标系
.以平面直角坐标系 为极点,
为极点,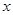 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线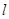 :
: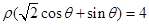 .
.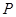 ,使点
,使点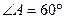 ,
,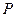 、
、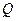 分别是
分别是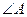 两边上的动点。
两边上的动点。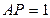 ,
,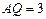 时,求
时,求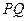 的长;
的长;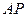 、
、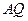 长度之和为定值4,求线段
长度之和为定值4,求线段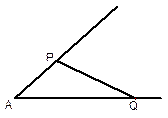

 通方程,并选择恰当的参数写出它的参数方程;
通方程,并选择恰当的参数写出它的参数方程; 在该圆上,求
在该圆上,求 的最大值和最小值.
的最大值和最小值.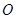 为原点,
为原点,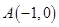 ,
,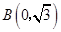 ,
,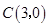 ,动点
,动点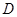 满足
满足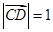 ,
,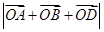 的取值范围是( )
的取值范围是( )
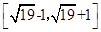
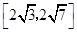
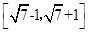

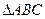 中,AB=AC,过点A的直线与其外接圆交
中,AB=AC,过点A的直线与其外接圆交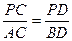 ;
;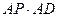 的值。
的值。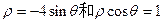 相交于点A、B,则|AB|= 。
相交于点A、B,则|AB|= 。