题目内容
函数f(x)=
-
的零点所在的区间为( )
| x |
| 2 |
| x |
分析:利用根的存在定理,分别判断,各区间端点处函数值的符合是否相反,从而确定零点所在的区间.
解答:解:函数f(x)=
-
在(0,+∞)上单调递增.
因为f(
)=
-4=
-4<0,f(1)=
-2=1-2<0,
f(
)=
-
=
-
<0,f(2)=
-1>0,
所以f(
)f(2)<0,
所以根据根的存在性定理可知函数f(x)=
-
的零点所在的区间为(
,2).
故选D.
| x |
| 2 |
| x |
因为f(
| 1 |
| 2 |
|
| ||
| 2 |
| 1 |
f(
| 3 |
| 2 |
|
| 4 |
| 3 |
| ||
| 2 |
| 4 |
| 3 |
| 2 |
所以f(
| 3 |
| 2 |
所以根据根的存在性定理可知函数f(x)=
| x |
| 2 |
| x |
| 3 |
| 2 |
故选D.
点评:本题主要考查函数与方程的关系,利用根的存在定理去判断函数零点所在区间,是解决本题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
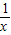 是奇函数”的证明不是综合法的是( )
是奇函数”的证明不是综合法的是( )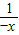 =-(x+
=-(x+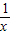 )=-f(x),∴f(x)是奇函数
)=-f(x),∴f(x)是奇函数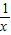 +(-x)+(-
+(-x)+(-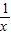 )=0,∴f(x)=-f(-x),∴f(x)是奇函数
)=0,∴f(x)=-f(-x),∴f(x)是奇函数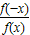 =
=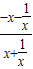 =-1,∴f(-x)=-f(x),∴f(x)是奇函数
=-1,∴f(-x)=-f(x),∴f(x)是奇函数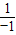 =-2,又f(1)=1+
=-2,又f(1)=1+ =2
=2