题目内容
18.曲线y=x3+2在点P(1,3)处的切线方程是( )| A. | 3x+y=0 | B. | 3x-y=0 | C. | 3x-y+6=0 | D. | 3x+y-6=0 |
分析 求出原函数的导函数,得到函数在x=1时的导数,即切线的斜率,然后由直线方程的点斜式得答案.
解答 解:由y=x3+2,得y′=3x2,
∴${y}^{′}{|}_{x=1}=3×{1}^{2}=3$,
即曲线y=x3+2在点P(1,3)处的切线的斜率为3,
∴曲线y=x3+2在点P(1,3)处的切线方程为y-3=3(x-1),
即3x-y=0.
故选:B.
点评 本题考查了利用导数研究过曲线上某点处的切线方程,过曲线上某点的切线的斜率,就是函数在该点处的导数值,是基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
6. 如图,空间四边形ABCD中,M、N分别是BC、DA上的点,且BM:MC=AN:ND=1:2,又AB=5,CD=3,MN与AB、CD所成的角分别为α,β,则之间的大小关系为( )
如图,空间四边形ABCD中,M、N分别是BC、DA上的点,且BM:MC=AN:ND=1:2,又AB=5,CD=3,MN与AB、CD所成的角分别为α,β,则之间的大小关系为( )
 如图,空间四边形ABCD中,M、N分别是BC、DA上的点,且BM:MC=AN:ND=1:2,又AB=5,CD=3,MN与AB、CD所成的角分别为α,β,则之间的大小关系为( )
如图,空间四边形ABCD中,M、N分别是BC、DA上的点,且BM:MC=AN:ND=1:2,又AB=5,CD=3,MN与AB、CD所成的角分别为α,β,则之间的大小关系为( )| A. | α<β | B. | α>β | C. | α=β | D. | 不确定 |
13.给出一下四个命题( )
①平面α外的一条直线l上有两个不同点到平面α的距离相等,则直线l平行于平面α
②平面α外有三个不共线的点到面α的距离相等,则经过这三个点的平面平行于平面α
③空间中垂直于同一直线的两直线可以不平行
④空间中垂直于同一平面的两个平面可以平行
其中真命题有( )
①平面α外的一条直线l上有两个不同点到平面α的距离相等,则直线l平行于平面α
②平面α外有三个不共线的点到面α的距离相等,则经过这三个点的平面平行于平面α
③空间中垂直于同一直线的两直线可以不平行
④空间中垂直于同一平面的两个平面可以平行
其中真命题有( )
| A. | ①②③④ | B. | ①②④ | C. | ②③④ | D. | ③④ |
7.等差数列{an}的首项a1=-5,它的前11项平均值为5,若从中抽去一项,余下的平均值为4.6,则抽去的是( )
| A. | a6 | B. | a8 | C. | a9 | D. | a10 |
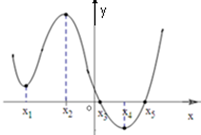 如图是导函数y=f′(x)的图象,在标记的点中,在哪一点处
如图是导函数y=f′(x)的图象,在标记的点中,在哪一点处 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,四边形BCC1B1是边长为6的正方形,直线AB与平面ACC1A1所成的角的正切值为3,点D为棱AA1上的动点,且AD>DA1.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,四边形BCC1B1是边长为6的正方形,直线AB与平面ACC1A1所成的角的正切值为3,点D为棱AA1上的动点,且AD>DA1.