题目内容
13.对任意x∈(0,$\frac{π}{2}$),不等式tanx•f(x)<f′(x)恒成立,则下列不等式错误的是( )| A. | f($\frac{π}{3}$)>$\sqrt{2}$f($\frac{π}{4}$) | B. | f($\frac{π}{3}$)>2cos1•f(1) | C. | f($\frac{π}{4}$)<2cos1•f(1) | D. | f($\frac{π}{4}$)<$\frac{\sqrt{6}}{2}$f($\frac{π}{6}$) |
分析 由题意可判断f(x)cosx在(0,$\frac{π}{2}$)上是增函数,从而依次判断不等式即可.
解答 解:∵对任意x∈(0,$\frac{π}{2}$),不等式tanx•f(x)<f′(x)恒成立,
∴对任意x∈(0,$\frac{π}{2}$),不等式$\frac{sinx}{cosx}$•f(x)-f′(x)<0恒成立,
∴对任意x∈(0,$\frac{π}{2}$),不等式sinx•f(x)-cosxf′(x)<0恒成立,
又∵(f(x)cosx)′=cosxf′(x)-sinx•f(x),
∴对任意x∈(0,$\frac{π}{2}$),不等式(f(x)cosx)′>0恒成立,
∴f(x)cosx在(0,$\frac{π}{2}$)上是增函数,
∴cos$\frac{π}{3}$f($\frac{π}{3}$)>cos$\frac{π}{4}$f($\frac{π}{4}$),
即f($\frac{π}{3}$)>$\sqrt{2}$f($\frac{π}{4}$),故A正确;
cos$\frac{π}{3}$f($\frac{π}{3}$)>cos1f(1),
即f($\frac{π}{3}$)>2cos1f(1),故B正确;
cos1f(1)>cos$\frac{π}{4}$f($\frac{π}{4}$),
即f($\frac{π}{4}$)<$\sqrt{2}$cos1•f(1)<2cos1•f(1),故C正确;
cos$\frac{π}{4}$f($\frac{π}{4}$)>cos$\frac{π}{6}$f($\frac{π}{6}$),
即f($\frac{π}{4}$)<$\frac{\sqrt{6}}{2}$f($\frac{π}{6}$),故D错误;
故选:D.
点评 本题考查了导数的综合应用及函数的单调性的判断与应用.

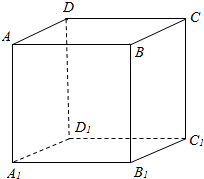 在正方体ABCD-A1B1C1D1的棱所在的直线中,与直线AB垂直的异面直线共有( )
在正方体ABCD-A1B1C1D1的棱所在的直线中,与直线AB垂直的异面直线共有( )| A. | 1条 | B. | 2条 | C. | 4条 | D. | 8条 |
| 级数 | 全月应纳税所得额 | 税率 |
| 1 | 不超过500元的部分 | 5% |
| 2 | 超过500元至2000元的部分 | 10% |
| 3 | 超过2000元至5000元的部分 | 15% |
(2)某人一月份应交纳税此项税款为26.78元,那么他当月的工资,薪金所得是多少?