题目内容
若数列{an}的前n项和为Sn,且满足Sn= an+1(n≥1),则an= ,
an+1(n≥1),则an= ,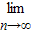 (a1+a2+a3+…+an)的值是 .
(a1+a2+a3+…+an)的值是 .
【答案】分析:在Sn= an+1(n≥1)①中,令n=1可得a1.当n≥2时,Sn-1=
an+1(n≥1)①中,令n=1可得a1.当n≥2时,Sn-1= an-1+1 ②,用①减去②,化简可得an=-
an-1+1 ②,用①减去②,化简可得an=- an-1,可得数列为等比数列,公比为-
an-1,可得数列为等比数列,公比为- ,
,
由此求得an.再根据等比数列的求和公式求得 Sn,可得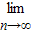 (a1+a2+a3+…+an)=
(a1+a2+a3+…+an)=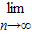 Sn 的值.
Sn 的值.
解答:解:由于数列{an}的前n项和为Sn,且满足Sn= an+1(n≥1)①,令n=1可得a1=
an+1(n≥1)①,令n=1可得a1= .
.
当n≥2时,Sn-1= an-1+1 ②,用①减去②,化简可得an=-
an-1+1 ②,用①减去②,化简可得an=- an-1,故数列为等比数列,公比为-
an-1,故数列为等比数列,公比为- ,∴an=
,∴an=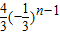 .
.
∴Sn=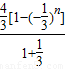 =1-
=1-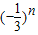 ,∴
,∴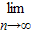 (a1+a2+a3+…+an)=
(a1+a2+a3+…+an)=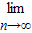 Sn=
Sn=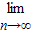 [1-
[1-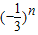 ]=1,
]=1,
故答案为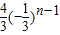 、1.
、1.
点评:本题主要考查数列的前n项和与第n项之间的关系,等比数列的求和公式,数列极限的运算法则的应用,属于中档题.
 an+1(n≥1)①中,令n=1可得a1.当n≥2时,Sn-1=
an+1(n≥1)①中,令n=1可得a1.当n≥2时,Sn-1= an-1+1 ②,用①减去②,化简可得an=-
an-1+1 ②,用①减去②,化简可得an=- an-1,可得数列为等比数列,公比为-
an-1,可得数列为等比数列,公比为- ,
,由此求得an.再根据等比数列的求和公式求得 Sn,可得
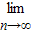 (a1+a2+a3+…+an)=
(a1+a2+a3+…+an)=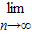 Sn 的值.
Sn 的值.解答:解:由于数列{an}的前n项和为Sn,且满足Sn=
 an+1(n≥1)①,令n=1可得a1=
an+1(n≥1)①,令n=1可得a1= .
.当n≥2时,Sn-1=
 an-1+1 ②,用①减去②,化简可得an=-
an-1+1 ②,用①减去②,化简可得an=- an-1,故数列为等比数列,公比为-
an-1,故数列为等比数列,公比为- ,∴an=
,∴an=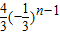 .
.∴Sn=
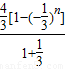 =1-
=1-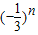 ,∴
,∴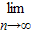 (a1+a2+a3+…+an)=
(a1+a2+a3+…+an)=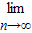 Sn=
Sn=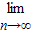 [1-
[1-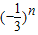 ]=1,
]=1,故答案为
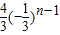 、1.
、1.点评:本题主要考查数列的前n项和与第n项之间的关系,等比数列的求和公式,数列极限的运算法则的应用,属于中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
